Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 4.Exercícios propostos - Ex. 8
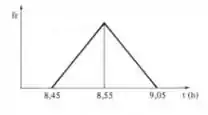
Uma pessoa deve chegar ao escritório onde trabalha até as horas. Devido ao tráfego e a fatores outros ele chega atualmente entre horas. A frequência relativa de suas diversas chegadas pode ser representada por um triângulo isósceles. Admitindo-se tal fato como verdadeiro, qual a probabilidade da pessoa não chegar atrasada?
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro do Mauri guerra de estática indutiva uma pessoa deve chegar ao escritório onde trabalha até as horas. Devido ao tráfego e a fatores outros ele chega atualmente entre horas. A frequência relativa de suas diversas chegadas pode ser representada por um triângulo isósceles. Admitindo-se tal fato como verdadeiro, qual a probabilidade da pessoa não chegar atrasada?
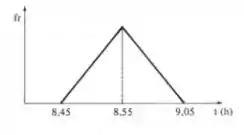
Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Para determinarmos a probabilidade com base no gráfico dado na questão, devemos saber que,
Vamos ficar com,
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.
Resposta