Um produtor de gelatina em pó está testando um novo lançamento e quer verificar em que condições de preparo o produto seria mais bem aceito. Vinte e quatro donas-de-casa atribuíram notas (0 a 10) para o prato que produziram com o produto. Junto com o produto foram fornecidos quatro tipos de receitas: duas para doces (A e D) e duas para salgados (B e C). Feita a análise estatística, quais recomendações você faria ao produtor? Discuta a validade das suposições feitas para resolver o problema.
Passo 1
Vamos lá.
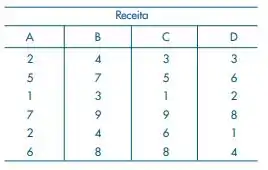
Esses são os dados do nosso problema.
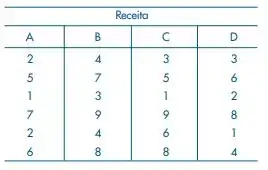
Queremos verificar em que condições de preparo o produto seria mais bem aceito. Para isso, vamos construir uma tabela ANOVA 😉.
Logo, temos um teste de comparação entre quatro médias. Como qualquer teste de hipótese, a primeira etapa é formular as hipóteses, para uma análise de variância, as hipóteses serão sempre assim:
Agora é partir para os cáculos.
Passo 2
Sabendo que
E calculando
Podemos montar nossa primeira tabelinha
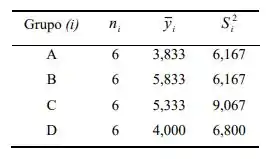
Olhando para as médias amostrais, vemos que elas têm valores diferentes, agora precisamos verificar se essa diferença é significativa, ou seja, se nós podemos dizer que baseados nessas diferenças que apareceram nas amostras, as populações são diferentes.
Vamos definir o nível de significância .
Passo 3
Agora, vamos calcular nossas informações que serão agrupadas numa única tabela, conhecida pelo nome de ANOVA, descrita na Tabela a seguir.

Basta aplicarmos as fórmulas que se encontram no Capítulo 10, calculando cada informação, temos
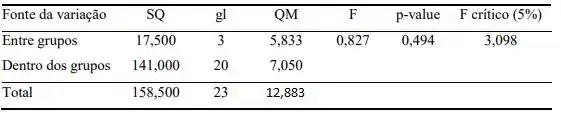
Para não perdemos tempo, na nossa tabela já constam os valores de F estatístico (0,827), p-valor (0,0494) e F crítico (3,098) uilizando um , beleza? 😉
Passo 4
Para finalizarmos, vamos usar a estatística F. Analisando a tabela F: p = 5%, temos que F crítico é igual a 3,098, portanto como F estatístico é menor que F crítico. Não rejeitamos , ou seja, concluímos que as notas médias dos 4 tipos de pratos são iguais.
Resposta
As notas médias dos 4 tipos de pratos são iguais. Logo, independente das condições de preparo o produto seria mais bem aceito ou não. No caso, olhando para as médias amostrais o produto não foi bem aceito, então é recomendado que o produtor reveja o lançamento da nova gelatina em pó.