No problema anterior, sorteando um funcionário ao acaso entre os 36:
(a) Qual será provavelmente o seu grau de instrução?
(b) E sua região de procedência?
(c) Qual a probabilidade do sorteado ter nível superior?
(d) Sabendo que o sorteado é do interior, qual a probabilidade de ele possuir nível superior? (e) Sabendo que o escolhido é da capital, qual a probabilidade de ele possuir nível superior?
Passo 1
Primeiro, precisamos da nossa tabela do problema anterior, né?
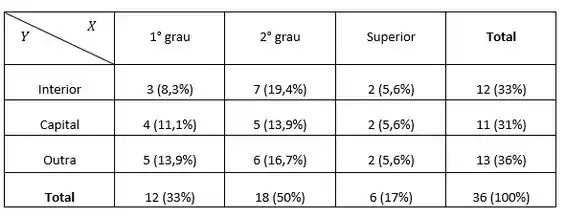
Agora vamos matar as nossas alternativas?
(a) Qual será provavelmente o seu grau de instrução?
1° grau tem um total de 12 funcionários, 2° grau 18 e superior 6.
Fica notório que no sorteio de um indivíduo dentre os 36, é maior a probabilidade de o mesmo ter o 2° 😉.
Passo 2
(b) E sua região de procedência?
Quanto à região de procedência, a maior probabilidade está associada com a região identificada por “Outra”.
Passo 3
(c) Qual a probabilidade do sorteado ter nível superior?
Basta olharmos para a nossa tabela.
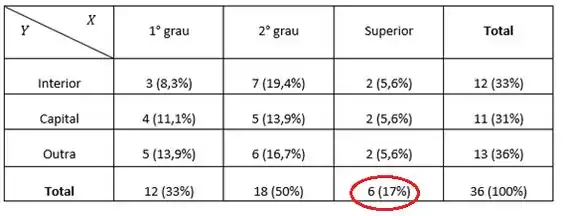
Logo
Passo 4
(d) Sabendo que o sorteado é do interior, qual a probabilidade de ele possuir nível superior?
Opa! Vocês concordam comigo que agora queremos uma probabilidade condicional?
Queremos , certo?
Sabemos que . Trazendo para o nosso problema, temos
Passo 5
(e) Sabendo que o escolhido é da capital, qual a probabilidade de ele possuir nível superior?
Seguindo a mesma ideia da altertativa “d”, temos
Resposta
(a) 2° grau.
(b) Outra.
(c) 17%
(d) 16,67%
(e) 18,18%