Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 6.Exercícios - Ex. 82
Reconsidere os dados do exercício 6-80. Prepare diagramas de caixa comparativos para os dois grupos de observações: 40 primeiros dados e os 40 últimos. Comente sobre a informação dos diagramas de caixa.
Passo 1
Primeiras 40 observações:
Vamos ordenar os valores dos dados do menor para o maior:
Já que o número de valores é par, a mediana é a média dos dois valores médios do conjunto de dados classificados:
O primeiro quartil é a mediana dos valores dos dados abaixo da mediana (ou em 25% dos dados):
O terceiro quartil é a mediana dos valores de dados acima da mediana (ou em 75% dos dados):
Passo 2
Próximas 40 observações:
Vamos ordenar os valores dos dados do menor para o maior:
Já que o número de valores é par, a mediana é a média dos dois valores médios do conjunto de dados classificados:
O primeiro quartil é a mediana dos valores dos dados abaixo da mediana (ou em 25% dos dados):
O terceiro quartil é a mediana dos valores de dados acima da mediana (ou em 75% dos dados):
Passo 3
Os whiskers (os fios de bigode) do boxplot estão no valor mínimo e máximo. A caixa começa no quartil inferior, termina no quartil superior e tem uma linha vertical na mediana.
O quartil inferior está em 25% da lista de dados classificados, a mediana em 50% e o quartil superior em 75%.
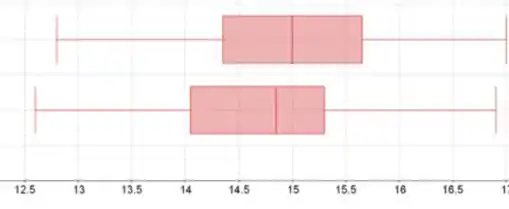
Ambas as distribuições parecem ser aproximadamente as mesmas.
O centro (mediana) para as primeiras 40 observações é ligeiramente menor do que o centro para as próximas 40 observações.
O grau de dispersão para os dois conjuntos de 40 observações parece ser aproximadamente o mesmo, porque a largura entre os whiskers é praticamente o mesmo para ambos os boxplots.
Resposta
O grau de dispersão para os dois conjuntos de 40 observações parece ser aproximadamente o mesmo, porque a largura entre os whiskers é praticamente o mesmo para ambos os boxplots.