A renda média disponível per capita no Colorado é de $13.901 (com base em dados do U.S. Bureau of Economic Analysis). Tom Phelps planeja abrir uma loja de revenda de carros Cadillac e quer verificar aquela cifra para determinada região do Colorado. Os resultados de uma pesquisa recentemente feita junto a 200 pessoas acusam média de $13.447 e desvio-padrão de $4883. Ao nível de 0,05 de significância, teste a afirmação de que a amostra foi extraída de uma população com renda média de $13.901. Há razão para Tom se preocupar com o nível de renda nessa região? Identifique também o valor P. Suponha que todas as amostras tenham sido extraídas aleatoriamente.
Passo 1
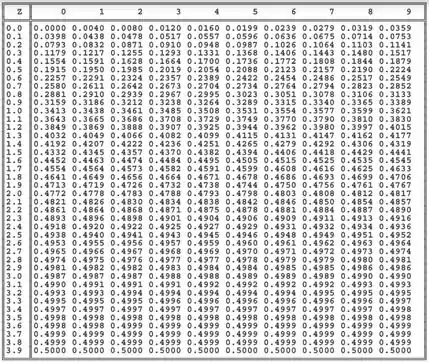
Tudo certo, pessoal? Bora continuar a fazer mais uns exercícios de teste de hipótese! São vários passos, mas não precisa ter medo! É só repetir o processo que estávamos fazendo! Vamos ter que usar uma tabela de distribuição normal de novo! Trouxe aqui uma imagem dela pra vocês!
Também vamos precisar usar a fórmula do Z para um Teste de Hipóteses para média (com conhecido ou ):
Primeiro, vamos determinar os valores iniciais do problema, montando e (já sabemos que o teste será bilateral porque vamos testar a hipótese ):
Passo 2
Show! Agora temos que encontrar o Z a partir da fórmula de antes:
Depois, chegamos ao valor P () correspondente ao Z encontrado na tabela. Como o valor de Z é negativo em um teste bilateral, temos que olhar para a porção esquerda do gráfico, já que buscamos a seguinte situação:
Vamos procurar os primeiros algarismos entre as linhas e o último entre as colunas. Assim, percebemos que, ao procurar por Z=-1,31, encontramos um valor de . Assim, vamos chegar a .
Passo 3
Tá quase! Agora, para acabar o teste de hipóteses, é só compararmos o valor de e . Nesse caso, e . Como o valor P () é maior que , concluímos que não podemos rejeitar . Assim, a afirmação está correta.
E pronto! Acabamos! Simples, né?
Resposta
e .
não é rejeitada. A afirmação está correta, logo Tom não tem razão para se preocupar com o nível de renda nessa região.