Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 11.Exercícios - Ex. 11

Os "resíduos" de uma ANOVA de dois fatores, com K i j = 1 são as quantidades x i j - μ ˆ + α ˆ i + β ˆ . Um gráfico de probabilidade normal desses resíduos pode ser usado para verificar a plausibilidade da hipótese de normalidade. Elabore esse gráfico usando os dados do Exemplo 11.1 e comente-o.

Passo 1

E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:

Os pares percentis residuais são:

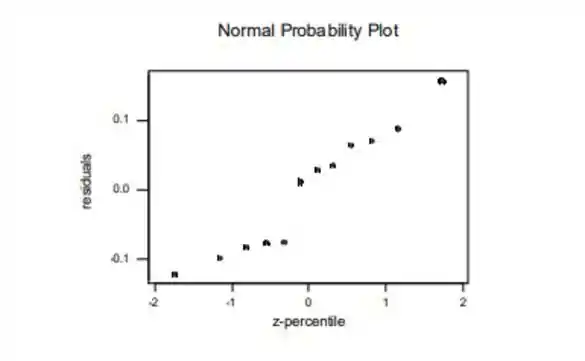
( - 0.1225 , - 1.73 ) , ( - 0.0992 , - 1.15 ) , ( - 0.0825 , - 0.81 ) , ( - 0.0758 , - 0.55 ) , ( - 0.0750 , - 0.32 ) , ( 0.0117 , - 0.10 ) , ( 0.0283,0.10 ) , ( 0.0350,0.32 ) , ( 0.0642,0.55 ) , ( 0.0708,0 . 81 ) , ( 0.0875,1.15 ) , ( 0.1575,1.73 ) .

O padrão é suficientemente linear, então a normalidade é plausível.

Resposta

O padrão é suficientemente linear, então a normalidade é plausível.

Exercícios de Livros Relacionados

Usando a tabela ANOVA, construída no Problema 5 :Construa o I C β ;90 % .
Idem para o problema 4 .
Investigando a relação entre a quantidade de fertilizante usado ( x ) e a produção de soja ( y ) numa estação experimental com 20 canteiros, obteve-se a equação de MQ: y ^ = 15,00 + 2,83 × x . 3,22 (
Usando a tabela ANOVA, construída no Problema 5 :d) Construa oI C para a acuidade visual média do grupo etário de 28 anos.
Para cada gráfico de resíduo abaixo, indique qual a possível transgressão observada.