Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 6º - Capítulo 9.Problemas - Ex. 22
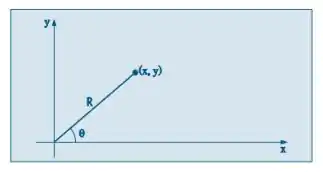
Transformação de Box-Müller. Considere as v.a. X e Y, independentes e ambas N(0, 1). Observando a Figura 9.10, vemos que R²= X²+ Y²e tgθ = Y/X. A densidade conjunta de X e Y é
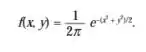
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrar os números aleatórios seguindo o método. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Considere a transformação de variáveis
A densidade conjunta de r e θ é obtida usando o resultado (8.28). Temos que x = √⎯r cosθ, y= √⎯r senθ e o Jacobiano da transformação é |J| = 1/2. Segue-se que a densidade de r e θ é
Passo 3
Dessa relação podemos concluir que r = R² e θ são independentes, com
Portanto, podemos escrever que
Aqui, usamos o fato de que, se R²~ Exp(2), gerado um NA U1, vem que –2log U1~ Exp(2) e se θ~U(0, 2π), então gerado um NA U2, vem que 2πU2~U(0, 2π).
Resposta
Ei, a resposta está no passo a passo :)