Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 2.Exercícios Suplementares - Ex. 92

Um transmissor está enviando uma mensagem usando código binário, ou seja, uma sequência de 0s e ls. Cada bit transmitido (0 ou 1) deve passar por três relés para chegar ao receptor. Em cada relé há uma probabilidade de 0,20 de que o bit enviado seja feito de forma diferente do bit recebido (uma reversão). Assuma que os relés operem de forma independente um do outro.

T r a n s m i s s o r   → R e l é   1   → R e l é   2   → R e l é   3   → R e c e p t o r

a. Se um 1 for enviado pelo transmissor, qual será a probabilidade de um 1 ser enviado por todos os relés?

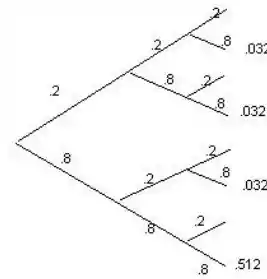
b. Se um 1 for enviado pelo transmissor, qual é a probabilidade de um 1 ser recebido pelo receptor? (Sugestão: Os oito resultados experimentais podem ser exibidos em um diagrama de árvore com três gerações de ramos, um para cada relé).

c. Suponha que 70% de todos os bits enviados do transmissor sejam 1. Se um 1 for recebido pelo receptor, qual é a probabilidade de um 1 ter sido enviado?

Passo 1

Beleza Pessoal?! Espero que sim, e espero também que você esteja super ligado para que juntos possamos resolver mais uma atividade de probabilidade.

  1. Como temos a probabilidade de 0.2 de o bit ser enviado diferente, isso quer dizer que temos a probabilidade de 0.8 de o bit ser enviado igual, então temos que

    2. P = 0.8 0.8 0.8 = 0.512

    Passo 2

    3. 0.512 + 0.032 + 0.023 + 0.023 = 0.608

  3. P   1   e n v i a d o   1   r e c e b i d o   ) = P ( 1   e n v i a d o   ∩ 1   r e c e b i d o ) P ( 1   r e c e b i d o ) = 0.4256 0.5432 = 0.7835

Resposta

  1. 0.512
  2. 0.608
  3. 0.7835

Exercícios de Livros Relacionados

Usando o princípio fundamental da contagem: Nos exercícios 25 a 28, use o princípio fundamental da contagem. 27. Imóvel Um corretor de imóveis utiliza uma caixa com segredo para guardar as chaves de u
Usando o princípio fundamental da contagem: Nos exercícios 25 a 28, use o princípio fundamental da contagem. 25. Menu Um restaurante oferece um jantar especial ao preço de $12 com 5 opções de entrada,
Encontrando probabilidades clássicas: Nos exercícios 29 a 34, um experimento probabilístico consiste em lançar um dado de 12 faces. Encontre a probabilidade do evento. 30. Evento B: sair um 10.
Encontrando probabilidades clássicas: Nos exercícios 29 a 34, um experimento probabilístico consiste em lançar um dado de 12 faces. Encontre a probabilidade do evento. 31. Evento C: sair um número mai
Classificando os tipos de probabilidade: Nos exercícios 41 a 46, classifique a afirmação como um exemplo de probabilidade clássica, empírica ou subjetiva. Explique seu raciocínio.41. De acordo com os