Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 2.5 - Ex. 26
Usando tecnologia para encontrar quartis e fazer gráficos - Nos exercícios 25 a 28, use a tecnologia para (a) encontrar o primeiro, o segundo e o terceiro quartis do conjunto de dados e (b) desenhar um boxplot que represente o conjunto de dados.
Dias de férias - O número de dias de férias em uma amostra de 20 funcionários em um ano recente.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A – Ordenando todos os valores
O mínimo (o menor valor de dado) é 0, a mediana é o valor do meio do conjunto de dados ordenado
O primeiro quartil é a mediana dos valores dos dados acima da mediana (ou em 75% dos dados):
O terceiro quartil é a mediana dos valores dos dados acima da mediana (ou em 75% dos dados):
O máximo (maior dado) é 10.
Passo 2
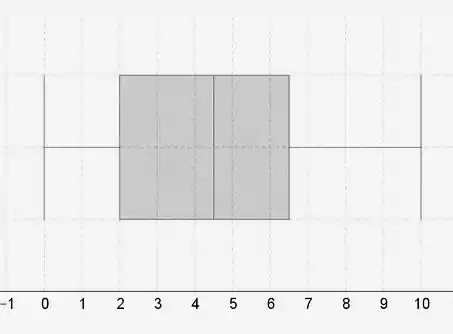
Os bigodes do boxplot estão no valor mínimo e máximo (não incluindo os outliers). A caixa começa no primeiro quartil, termina no terceiro quartil e tem uma linha vertical na mediana.
O primeiro quartil está em 25% da lista de dados classificados, a mediana em 50% e o terceiro quartil em 75%.
