Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 7.3 - Ex. 3
Uma variável aleatória assume quatro valores com igual probabilidade. Para uma amostra de tamanhos dois, obtenha a distribuição de e verifique se ele é não viesado para estimar a variância da variável.
Passo 1
Oi, tudo bem? Vamos construir uma tabela para a distribuição de , considerando a amostra Lembrou-se que:
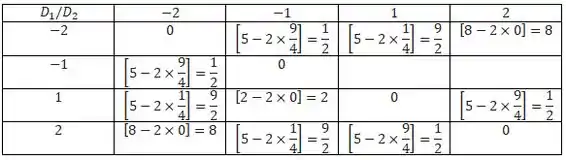
Passo 2
Assim, a distribuição de probabilidade de é:
O valor esperado deste estimador é:
Que é a variância da população.
Resposta
Assim, não é viesado.
Exercícios de Livros Relacionados
Reconsidere o exercício 16-5. Use os limites revistos de controle e as estimativas de processo.a)Estime R C P e R C P i e interprete essas razões.b)Que porcentagem de defeitos está sendo produzida por
A tabela seguinte de dados foi analisadada. O tamanho médio de partícula da matéria-prima foi obtido a partir de 25 amostras sucessivas.a)Usando todos os dados, calcule os limites tentativas de contro
O teor de cobre de um banho de chapeamento é medido três vezes ao dia, sendo os resultados reportados em ppm. Os valores de x e r para 25 dias são mostrados na seguinte tabela:a)Usando todos os dados,
Monitora-se a resistência à tração de um fio de chumbo colado a uma placa de circuito integrado. A seguinte tabela fornece dados para 20 amostras, cada uam de tamanho três.a)Usando todos os dados, enc
A viscosidade de um intermedirário químico é medida a cada hora. Vinte amostras, cada uma de tamanho n = 1 , estão na seguinte tabela.a)Usando todos os dados, calcule os limites tentativas de controle