O verdadeiro valor de um diploma de curso superior não pode ser medido quantitativamente, mas há maneiras de avaliá-lo em termos de renda. Os homens que têm apenas o curso secundário têm uma renda média anual de $21.652. Selecionados aleatoriamente 73 homens com diploma de faculdade, sua renda média anual é de $40.202 e o desvio-padrão é de $10.900 (com base em dados do Department of Labor - EUA). Ao nível de 0,01, teste a afirmação de que os homens com diploma de faculdade têm renda média anual superior à dos que têm apenas o curso secundário. Como responderia a quem arguísse que o tamanho da amostra 73 é demasiadamente pequeno neste caso? Identifique também o valor P.
Passo 1
Tudo certo, pessoal? Bora continuar a fazer mais uns exercícios de teste de hipótese! São vários passos, mas não precisa ter medo! É só repetir o processo que estávamos fazendo! Vamos ter que usar uma tabela de distribuição normal de novo! Trouxe aqui uma imagem dela pra vocês!
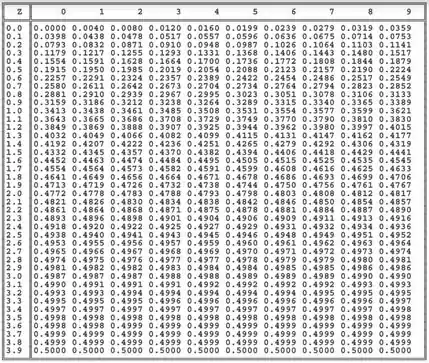
Também vamos precisar usar a fórmula do Z para um Teste de Hipóteses para média (com conhecido ou ):
Primeiro, vamos determinar os valores iniciais do problema, montando e (já sabemos que o teste será unilateral direito porque vamos testar a hipótese ):
Passo 2
Show! Agora temos que encontrar o Z a partir da fórmula de antes:
Depois, chegamos ao valor P () correspondente ao Z encontrado na tabela, já que buscamos a seguinte situação:
Eita! Nesse caso nosso é bem grande e não consta na tabela, logo teremos que assumir o valor associado 0,5 aqui. Assim, chegamos a .
Passo 3
Show! Agora pra acabar o teste de hipóteses, é só compararmos o valor de e . Nesse caso, e . Como o valor P () é menor que , concluímos que devemos rejeitar . Assim, a afirmação está correta.
E pronto! Acabamos! Simples, né?
Resposta
e . é rejeitada. A afirmação está correta.
O tamanho da amostra de 73 pode parecer pequeno, mas a diferença da renda anual média dos dois grupos é tão gritante que, mesmo com um número relativamente pequeno de amostra, o teste ainda comprova adequadamente a diferença das médias.