Leis de De Morgan. Neste capítulo, discutimos os operadores lógicos &&, || e !. Às vezes, as Leis de De Morgan podem tornar mais conveniente a indicação de uma expressão lógica. Essas leis afirmam que a expressão !(condition1 && condition2) é logicamente equivalente à expressão (!condition1 || !condition2). Além disso, a expressão !(condition1 || condition2) é logicamente equivalente à expressão (!condition1 && !condition2). Use as Leis de De Morgan para escrever expressões equivalentes para cada um dos seguintes itens, e depois escreva um programa para mostrar que a expressão original e a nova expressão em cada caso são equivalentes.
Passo 1
Essa questão pede uma base matemática mais profunda, que geralmente é vista na cadeira de Matemática Discreta ou outra equivalente. De qualquer forma, o próprio enunciado nos dá o conhecimento necessário para responder todas as perguntas :D Vamos entender cada uma?
Primeiro, é bom saber que:
! – valor lógico oposto
&& - “e”
|| - “ou”
A primeira equivalência é que o valor oposto entre condição 1 e condição 2 é igual ao oposto da condição 1 ou o oposto da condição 2. Tá, mas isso não te diz nada, né? Olha o esquema abaixo:
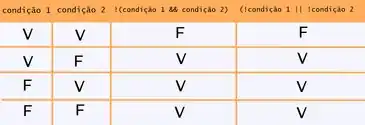
Basicamente, considerando, por exemplo, que ambas as condições sejam verdadeiras, condição 1 && condição 2 é verdadeiro. Por isso, !( condição 1 && condição 2) é falso. Da mesma forma, !condição 1 vale falso e !condição 2 vale falso. Falso ou falso resulta em falso. Logo, ambas têm o mesmo valor lógico. Deu pra pegar a ideia?
Da mesma forma, podemos fazer para a equivalência entre !(condição 1 || condição 2) e (!condição 1 && !condição 2):

Pronto! Estamos armados para resolver problemas!
Passo 2
- A expressão !( x = 7 ) tem o formato (!condição 1 && !condição 2). Portanto, sua equivalência lógica tem a forma !(condição 1 || condição 2). Nesse caso, sabendo que a condição 1 é x = 7, então teremos como resposta entre !( x =7 ).
- Nesse item, temos a expressão !( a == b ) || !( g != 5 ). Ela tem o formato !( condição 1) || !( condição 2 ). Portanto, a equivalência, conforme a tabela, tem a forma !( condição 1 && condição 2). Logo, o resultado é !( a == b && g != 5).
- Temos a expressão !( ( x 4 ) ) que é da forma !( condição 1 && condição 2) logo sua equivalência é !( condição 1) || !( condição 2 ). A resposta, então, é !(x 4 ).
- Por último, temos que !( ( i > 4 ) || ( j 4) && !(j
Passo 3
Passo 4
Passo 3
Resposta
- !( x =7 )
- !( a == b && g != 5)
- !(x 4 )
- !(i > 4) && !(j