Diagrama de Bode
Produzido por Alexandre NunesTeoria
No diagrama de bode representamos razão de amplitude
📢 Clique para ver mais:
Ele tem essa carinha aqui:
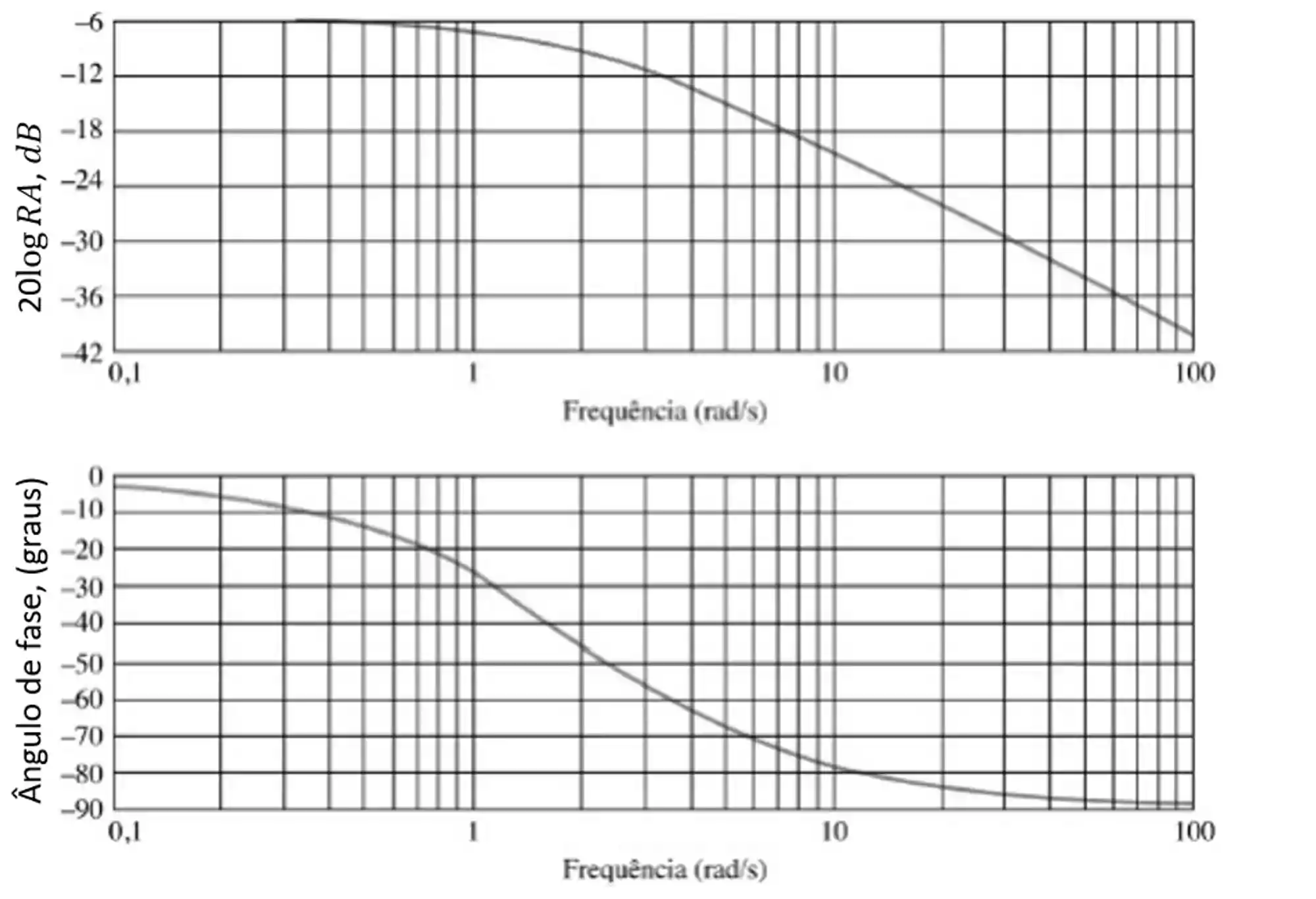
O primeiro gráfico é o de razão de amplitude, entretanto, com o objetivo de facilitar os cálculos e as representações gráficas, muitas vezes opta-se por representar
Quando fazemos essa modificação, chamamos a unidade de decibel
O segundo gráfico representa o ângulo de fase, em graus, em função do
Vamos entender um pouco melhor esse tal de diagrama de Bode e ainda ver algumas técnicas de como esboçar esses diagramas?
Traçado por assíntotas: Razão de amplitude
O diagrama de Bode pode ser esboçado de maneira aproximada a partir de uma sequência de retas, e é nisso que focaremos a partir de agora. Vamos continuar usando a seguinte função:
Sempre que formos fazer o traçado por assíntotas do diagrama de bode, será interessante representar os polos e zero com um “mais um”, então vamos dividir toda a equação por
Então:
Muitas vezes a curva é feita em decibéis, ou seja:
Vamos usar propriedades logarítmicas para manipular um pouco essa expressão:
Ou seja, a curva de
que é uma constante, já que não depende da frequência variável, em função da frequência .
Para a segunda curva, vamos analisar o que acontece em altas e em baixas frequências.
Baixas Frequências de Entrada
Se temos baixas frequências de entrada, podemos dizer que:
Então podemos desprezar o termo da frequência e a expressão fica:
Ficamos então com:
Ou seja, em frequências muito baixas o polo não impacta na razão de amplitude.
Altas Frequências de Entrada
Agora é o inverso, temos altas frequências de entrada, então:
Fazemos a seguinte aproximação:
Substituindo na expressão para
Ou seja, em altas frequências, esse termo se comporta como uma reta de inclinação
Esboço do Diagrama de Bode
Vamos colocar isso no diagrama para entender melhor onde queremos chegar:
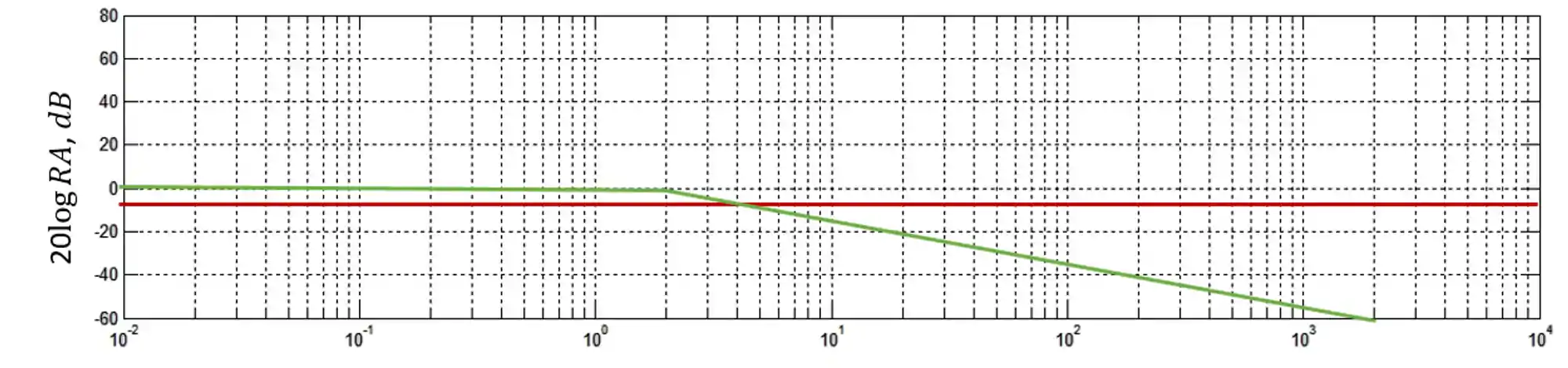
Nós vimos que a expressão para
Nesse gráfico representamos em vermelho o primeiro termo,
Nós dizemos que a reta tem inclinação
Como o gráfico da razão de amplitude é uma soma desses dois termos (ou dessas duas retas), para desenhar então a versão final só nos resta juntar as duas retas:
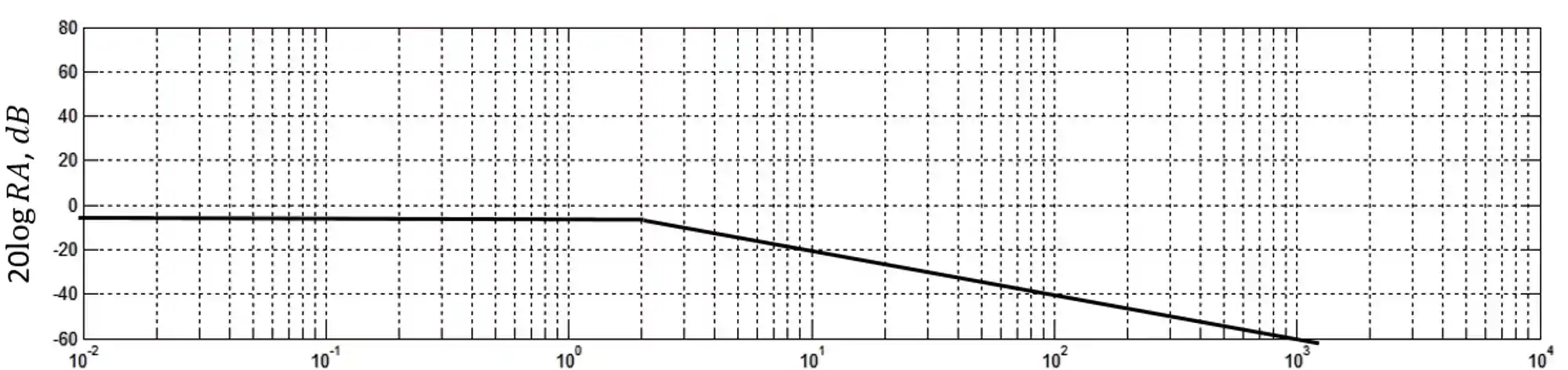
Em baixas frequência, a razão de amplitude só é impactada por
Prontinho! Agora vamos praticar com exercícios?