Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 16.Problemas - Ex. 106

106 - Um tanque com volume constante contém 1   k m o l de oxigênio de carbono C O e 3   k m o l de oxigênio O 2 (nenhum nitrogênio) a 25   °   C e 3   a t m . A mistura é então inflamada, e o C O queima completamente até formar dióxido de carbono C O 2 . Para determinar a temperatura final do tanque de 800   K , determine uma pressão final no tanque e a quantidade de calor transferida. É razoável considerar que não haverá C O no tanque quando o equilíbrio químico for atingido?

Passo 1

Pois bem, precisamos começar esse problema escrevendo a equação estequiométrica para a reação. Sabemos do enunciado que estamos queimando monóxido com 3   k m o l de oxigênio...

C O + 3 O 2

E a queima acontece totalmente, ou seja, por balanceamento...

C O + 3 O 2 →                                     C O 2 + 2,5 O 2

Passo 2

Show! Sabemos que há a variação de pressão no problema, logo a troca de calor com o exterior pode ser dada por essa equação aqui:

Q = ∑ N R h - f 0 + h - - h - 0 - P v - R - ∑ N P h - f 0 + h - - h - 0 - P v - P

Como se trata de gases ideais...

P v - = R u T

Então...

Q = ∑ N R h - f 0 + h - - h - 0 - R u T R - ∑ N P h - f 0 + h - - h - 0 - R u T P

Ora bolas! Conhecemos as temperaturas dos reagentes ( 25 ° C ou 298 K ), assim como conhecemos a temperatura do produto ( R u é a constante dos gases)...

Q = ∑ N R h - f 0 + h - - h - 0 - 8,314 ⋅ 298 R - ∑ N P h - f 0 + h - - h - 0 - 8,314 ⋅ 800 P

Como temos 2 reagente e dois produtos, podemos desmembrar assim...

Q = 1 h - f 0 + h - - h - 0 - 8,314 ⋅ 298 C O + 3 h - f 0 + h - - h - 0 - 8,314 ⋅ 298 O 2 - 1 h - f 0 + h - - h - 0 - 8,314 ⋅ 800 C O 2 - 2,5 h - f 0 + h - - h - 0 - 8,314 ⋅ 800 O 2

Como o monóxido de carbono e o oxigênio dos reagentes estão a   25 ° C ( 298 K ) então podemos cancelar h - - h - 0 deles...

Q = 1 h - f 0 - 8,314 ⋅ 298 C O + 3 h - f 0 - 8,314 ⋅ 298 O 2 - 1 h - f 0 + h - - h - 0 - 8,314 ⋅ 800 C O 2 - 2,5 h - f 0 + h - - h - 0 - 8,314 ⋅ 800 O 2

Avaliando a tabela agora...

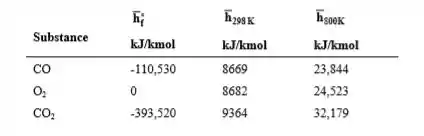
E substituindo-se tudo...

Q = 1 - 110530 - 8,314 ⋅ 298 + 3 0 - 8,314 ⋅ 298 - 1 - 393520 + 32179 - 9364 - 8,314 ⋅ 800 - 2,5 0 + 24523 - 8682 - 8,314 ⋅ 800 →

Q = - 233940   k J / k m o l

Ou, podemos falar que a quantidade de calor transferida é 233940   k J / k m o l .

Passo 3

Para determinar a pressão final, podemos assumir que estamos trabalhando com os gases ideias, portanto é válida a relação...

P 1 V P 2 V = N 1 R u T 1 N 2 R u T 2     →

Como o volume está fixo...

P 1 = N 1 T 1 N 2 T 2   P 2

Considerando o 2 como sendo a etapa inicial (onde só tínhamos os reagentes) e o 1 a etapa final onde agora temos os produtos, já podemos substituir as temperaturas e P 2 (pressão dos reagentes):

P 1 = N 1 ⋅ 800 N 2 ⋅ 298   3

Já em relação ao número de mols, vejamos novamente a equação da reação...

C O + 3 O 2 →                                     C O 2 + 2,5 O 2

Bem, perceba que a quantidade de mols dos reagentes é N 2 = 1 + 3 = 4   k m o l , e já a quantidade dos produtos... N 1 = 1 + 2,5 = 3,5   k m o l . Então...

P 1 = 3,5 ⋅ 800 4 ⋅ 298   3 =

7,05   a t m

Passo 4

Pois bem, a constante de equilíbrio para a reação...

C O 2 → C O + 1 2 O 2

Em 800 K é (consultando a tabela A - 28 )...

  ln ⁡ K p = - 37,2

Portanto, a formação de C O   a partir de C O 2 é extremamente improvável, por K p se tratar de um número absurdamente pequeno! Logo, é sim razoável dizer que não haverá a produção de C O .

Resposta

Q = - 233940   k J / k m o l

P = 7,05   a t m

Ver Outros Exercícios desse livro