Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 16.Problemas - Ex. 96
96 - Gás metano é queimado com de excesso de ar. Esse combustível entra em um combustor em regime permanente a e e é misturado com o ar. Os produtos de combustão saem desse reator a e . Determine a composição de equilíbrio dos produtos de combustão e a quantidade de calor liberado por essa combustão, em de metano.
Passo 1
Pois bem, a primeira coisa que devemos fazer em um problema como esse, claro, considerando um problema de gases ideais, é montar a equação estequiométrica do problema. Como se trata da queima do gás metano...
Beleza, mas essa não é a equação real do que está acontecendo no nosso problema. Para montar a equação real a gente tem que levar em conta o fato de que o ar é composto de nitrogênio também. Vamos montar então a equação real?
Passo 2
Ora bolas, o ar é composto de de oxigênio para de Nitrogênio...
E esses dois compostos juntos, em temperaturas altas, ele podem formar !
Então, a queima real do metano, sabendo que temos que ter a mais de ar será dado por...
Perceba que colocamos , por que a queima original demanda duas molécula de oxigênio, mas como precisamos de a mais de ar...
Saca?
são as porcentagens de cada composto. E encontrara-las é o que devemos fazer! Mas antes, perceba que já temos as porcentagens de dióxido de carbono e agua, afinal, a queima do metano a uma alta temperatura, acontece devido o baixo valor de . Logo, os únicos valores que realmente precisamos encontrar são os da transformação de...
Na temperatura de .
Passo 3
Bem, pela estequiometria acima, podemos tirar que...
O número de moles de cada um deles presentes na queima do metano é dado pelo balanço químico...
Portanto...
Isolando e em função de ...
Logo, o número de moles de , e é dado respectivamente...
Enquanto que o número total de moles é dado por...
Só falta uma coisa agora antes de correr para a fórmula... Determinar o valor da constante de dessa reação! De acordo com a tabela A-28...
Como temos o dobro em relação à fórmula da tabela:
Então, no nosso caso...
Passo 4
Podemos agora substituir na fórmula de ...
Substituindo-se tudo (lembre-se que )...
Simplificando...
Passando multiplicando...
Passando tudo para um lado só...
E resolvendo essa equação do segundo grau...
Enquanto que...
Logo, podemos concluir que a equação da queima do metano é...
Passo 5
Sabemos que o calor liberado é dado pela variação de energia no sistema da queima:
Que pela lei da termodinâmica...
Além disso, a variação de energia do pode ser dado como a variação de entalpia :
Como não tem trabalho na nossa queima, a variação de calor total já será dada pela variação de entalpia...
Assumindo o ar e a combustão como gases ideais, o nosso de formação dos produtos... Resume-se há...
Perceba que pelo fato de desprezamos o produto , ok?
Tomando então essa tabelinha aqui...
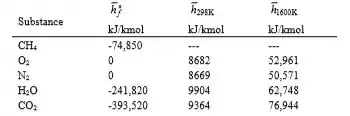
E substituindo-se que são as quantidade de moles envolvidos...
Então, a quantidade de energia na queima é...