Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 2.Problemas - Ex. 74
Água e bombeada de um reservatório mais baixo para um reservatório mais alto por uma bomba que fornece de potência de eixo. A superfície livre do reservatório superior está acima daquela do reservatório inferior. Considerando que a vazão da água é de , determine a potência mecânica convertida em energia térmica durante esse processo devido aos efeitos do atrito.
Passo 1
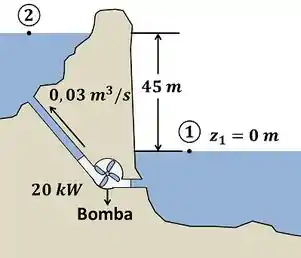
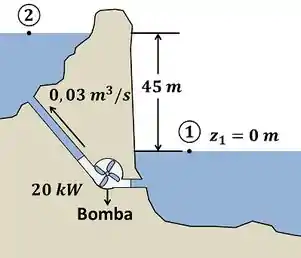
O enunciado diz que a bomba consome para fazer a água passar de um reservatório mais baixo para um reservatório mais alto. Isso quer dizer que a única função dessa bomba é aumentar a energia potencial da bomba. O problema é que parte dos que a bomba recebe do eixo não contribuem para a variação da energia potencial. Parte se perde por atrito. É essa perda que o enunciado quer que a gente calcule! A figura abaixo mostra todas as informações que a questão nos dá para calcular essa parte perdida por atrito.
Ou seja, a quantidade de energia que a bomba desperdiça por segundo devido ao atrito é igual à energia total que ela recebe por segundo menos a energia que ela dá pra água na forma de energia potencial .
é dado pelo enunciado e evale .
precisa ser calculado. Ele é a variação de energia potencial. A sua fórmula será mostrada e explicada no próximo passo.
Passo 2
onde é a aceleração da gravidade da Terra que vale , é a variação de altura da água do reservatório mais baixo pro reservatório mais alto e é a vazão mássica de água.
O valor de é mostrado na figura. Quando a água se desloca do ponto para o ponto , ela se eleva em .
Já precisa ser calculado a partir da vazão volumétrica da água dada pelo enunciado. Convertemos em , multiplicando pela densidade da água .
A vazão volumétrica da água é dada pela questão.
Atenção! O exercício não fala quanto vale o da água líquida a temperatura ambiente. Mas podemos considerar que ele vale !
Agora vamos para o passo final de cálculo de .
Passo 3
Começamos calculando a vazão mássica .
A segunda etapa é calcular a variação de energia potencial .
Por fim, calculamos o que o exercício pede .