Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 02
Água entra na caldeira de uma máquina de Carnot com escoamento em regime permanente como líquido saturado a , saindo com um título igual a . Vapor sai da turbina a uma pressão de . Mostre o ciclo em um diagrama T-s em relação às linhas de saturação e determine (a) a eficiência térmica, (b) o título no final do processo isotérmico de rejeição de calor e (c) o trabalho líquido produzido.
Passo 1
Temos três letrinhas pra resolver e um diagrama para montar. Vamos lá!
Começando pela nossa letra (a), primeiro a gente precisa separar as temperaturas correspondentes para cada pressão dada pra gente:
A nossa temperatura correspondente a é o nosso e a de o nosso , e os dois devem Rankine para as unidades estarem ajustadas, então vamos arrumar:
Show! agora já podemos encontrar a nossa eficiência:
ou
Passo 2
Agora partiu letra (b)! O exercício pede o título final do processo isotérmico, vamos encontrá-lo!
Bom, o nosso título final é o , como estamos em um ciclo fechado ele é igual ao nosso e os dois serão iguais ao , beleza? Então eles serão:
Agora tá show! É só a gente colocar na fórmulinha para achar o título final e substituir com os valores que já são tabelados:
Sabendo que:
Podemos resolver! Vamos lá:
Uhul! Agora só falta a última parte!
Passo 3
Na letra (c), ele quer o trabalho líquido produzido, ele é dado por essa fórmula aqui:
A eficiência a gente encontrou lá na letra A, então temos que achar o . Vamos lá!
Nós temos o mas precisamos achar o , então vamos começar por aí!
O é o nosso próprio , o a questão nos deu lá no enunciado e o é tabelado, então é só colocar ali e achar o que precisamos:
Agora podemos voltar lá na fórmula do :
E finalmente...O trabalho líquido!
Passo 4
Partiu montar nosso diagrama:
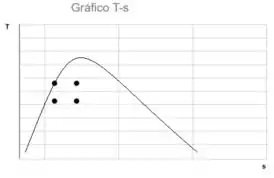
Resposta
