A água é utilizada como fluido de trabalho em um ciclo ideal regenerativo de Rankine. O vapor superaquecido entra na turbina a e , e a pressão no condensador é de . O vapor se expande ao longo da turbina no primeiro estágio até , na qual uma certa quantidade de vapor é extraída e desviada para um aquecedor de alimentação aberto que opera a . O vapor remanescente se expande ao longo da turbina no segundo estágio até a pressão de no condensador. O líquido saturado sai do aquecedor de água de alimentação a . Determine para esse ciclo:
- A taxa de adição de calor, em por de vapor que entra na turbina no primeiro estágio
- A eficiência térmica
- A taxa de transferência de calor do fluido de trabalho ao passar pelo condensador para a água de resfriamento, em por de vapor que entra na turbina do primeiro estágio.
Passo 1
E aí, galerinha! Oia nós aqui de novo!
Bom! Mais aí um exercício sobre sistemas de vapor e turbinas, especialmente, turbinas!
E como é de praxe nesse tipo de exercício, a primeira coisa a se fazer, é um esboço do ciclo e do nosso sistema! Isso vai nos ajudar a entender melhor o nosso problema!
Vamos começar construindo o gráfico do ciclo de temperatura :
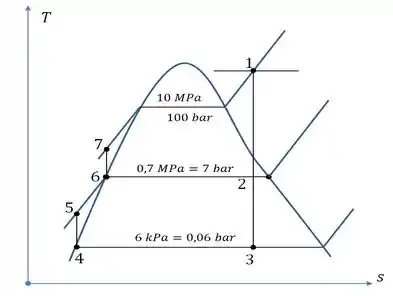
Que beleza de imagem, né não?
Passo 2
Agora, com base em tabelas como a do livro, mostrada abaixo...
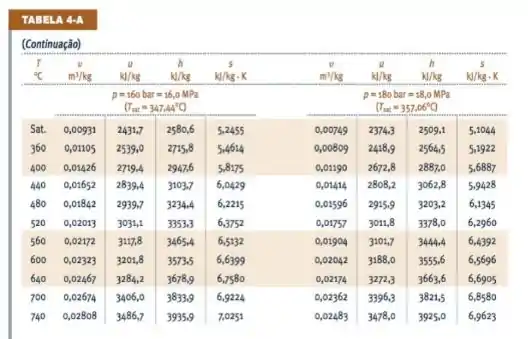
Vamos encontrar as condições referentes aos principais estados destacados na figura do final do !
Para o estado onde , ; temos que:
Para o estado onde , ; temos que:
Passo 3
Para o estado , da tabela, temos que...
Dessa forma, calculando ;
Para o estado , com líquido saturado, temos que...
Passo 4
E finalmente para o estado , falta achar . Pela figura, podemos ver que...
Dessa forma, substituindo os valores numéricos...
Para o estado , com líquido saturado, temos que...
Por último, para o estado , falta achar . Pela figura, podemos ver que...
Dessa forma, substituindo os valores numéricos...
Passo 5
a) Que beleza! A parte mais complicadinha já foi! Agora, vamos tratar de achar a eficiência!
Analisando o ciclo na figura do , temos que o trabalho do ciclo dividido pela vazão mássica fica assim...
A taxa de adição de calor, em por de vapor que entra na turbina no primeiro estágio
pode ser reescrito como...
O que nada mais é do que escrever em termos das entalpias que temos!
Assim, substituindo os valores numéricos...
b) Agora, vamos encontrar a eficiência. Aplicando o balanço de energia, temos que...
Sendo assim, para o volume de controle que engloba a turbina, temos que...
Para as bombas, por sua vez, o trabalho vai ser dado por...
Calculando então, o trabalho geral...
Podemos achar a eficiência assim...
c) Por fim, falta achar a transferência de calor do fluido de trabalho que passa pelo condensador...
Bom! Pelo que podemos ver, ela é dada por...
Pronto! Sucesso, meus queridos!
Resposta
a)
c)
d)