apor a 400 lbf/in2 (2,8 MPa) e 600ºF (315,6ºC) entra em uma turbina bem isolada que opera em regime permanente e sai como vapor saturado a uma pressão p.
(a) Para p = 50 lbf/in2 (344,7 kPa), determine a taxa de destruição de exergia, em Btu por lb de vapor em expansão através da turbina, e as eficiências exergética e isentrópica da turbina.
(b) Esboce graficamente a taxa de destruição de exergia, em Btu por lb de vapor, e as eficiências exergéticas isentrópicas, versus a pressão p variando de 1 a 50 lbf/in2 (6,9 a 344,7 kPa). Ignore os efeitos de movimento e gravidade, e adote T0 = 60ºF ( 15,6°C) e p0 = 1 atm.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de física quântica?!
Passo 2
Desenhando a curva para a turbina
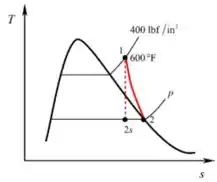
Passo 3
a) para
calculando a eficiência isentrópica da turbina
Obtendo as propriedades do vapor da Tabela A-4E. A pressão de e temperatura de
Obtendo as propriedades do vapor da Tabela A-3E. A pressão de
Passo 4
Considerando o processo 1-2s (processo de expansão isentrópica). A entropia permanece constante durante o processo
Passo 5
Calculando a entalpia no estado 2s
Calculando a eficiência isentrópica
Passo 6
Calculando a taxa de destruição de exergia na turbina
Passo 7
Considerando um volume de controle na turbina e opera em um estado estacionário. Então, para o volume de controle, não há transferência de calor no sistema ou para o sistema e os efeitos de energia potencial e cinética não negligenciadas
Considerando o balanço de energia no volume de controle
Passo 8
Calculando a eficiência de exergia da turbina
Passo 9
b) repetindo o mesmo procedimento para diferentes valores de pressão de saída (variando de 1 a 50 psi) e calculando a eficiência isentrópica, a taxa de destruição de exergia na turbina e a eficiência de exergia da turbina
A tabela representando os valores obtidos para a eficiência isentrópica (), e para diferentes valores de pressão de saída ()
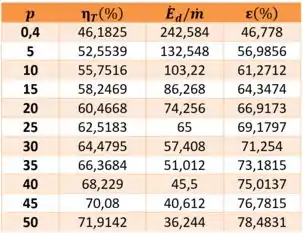
Passo 10
Gerando gráficos
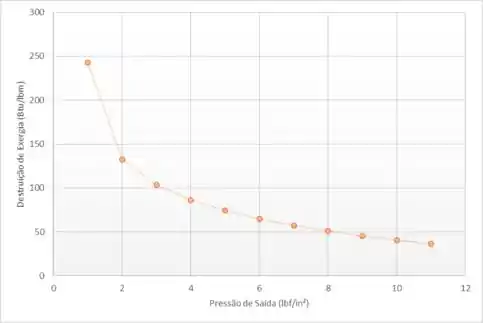
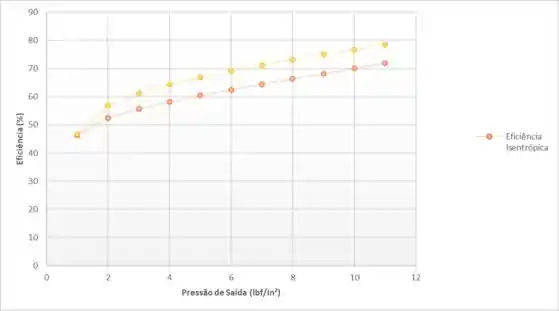
Passo 11
Resolvendo para
Passo 12
Tabulando os calores variando de 0 a 0,5
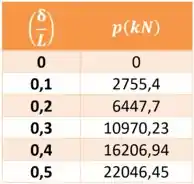
Plotando, temos que
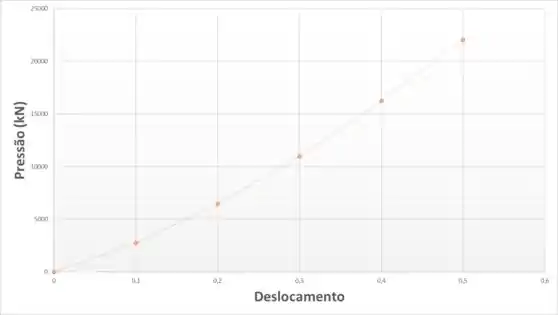
Resposta
Ei, a resposta está no passo a passo :)