Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 4.Problemas - Ex. 80
Um arranjo pistão-cilindro, com batentes na parte superior, contém inicialmente 3 kg de ar a 200 kPa e 27 °C. Calor é então transferido para o ar e o pistão sobe até atingir os batentes, e nesse ponto o volume é duas vezes o volume inicial. Mais calor é transferido até que a pressão dentro do cilindro também dobre. Determine o trabalho realizado e a quantidade de calor transferido nesse processo. Mostre também o processo em um diagrama P-v.
Passo 1
Nesse problema, pode-se negligenciar as variações de energia potencial e de energia cinética no sistema. Logo, a equação de balanço de energia para o sistema é:
O diagrama P-v que representa os processos que ocorrem no sistema é:
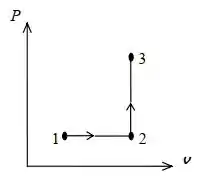
Passo 2
O volume inicial do ar é dado por (R = 0,287 kPa.m³/kg.K):
O volume final é dado por:
A temperatura final no sistema é:
Passo 3
Temos que durante o processo 1-2, o sistema realiza trabalho sobre a fronteira, com a pressão constante, e é dado por:
As energias internas do ar no início e no final dos processos podem ser obtidas na Tabela A-17:
Assim, o calor total transferido no processo é: