Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 5.Problemas - Ex. 192

Um arranjo pistão-cilindro contem inicialmente 2 kg de refrigerante-134a a 800 kPa e 80ªC. Nesse estado, o pistão toca um par de batentes na parte superior do cilindro. A massa do pistão é tal que é necessária uma pressão de 500 kPa para movê-lo. Uma válvula na parte inferior do tanque é então aberta, e R-134a é retirado do cilindro. Após algum tempo, observa-se que o pistão se move e a válvula é fechada quando metade do refrigerante é retirado do tanque; além disso, a temperatura deste cai para 20ºC. Determine (a) o trabalho realizado e (b) a transferência de calor.

Passo 1

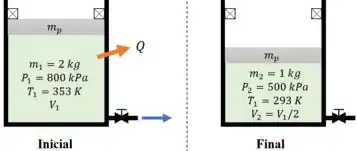
Como a questão afirma, pro pistão se mover é necessária a pressão de 500   k P a , então, podemos afirmar que a pressão final é:

P 2 = 500   k P a

Para efetuar os cálculos precisaremos determinar o volume específico, a entalpia e a energia interna do fluido.

P 1 = 800   k P a T 1 = 80     º C m 1 = 2   k g ⇒ T a b e l a   A - 13 v 1 = 0,032659   m 3 / k g u 1 = 290,84   k J / k g h 1 = 316,97   k J / k g

P 2 = 5 00   k P a T 2 = 2 0     º C m 2 = 1   k g ⇒ T a b e l a   A - 13 v 2 = 0,042155   m 3 / k g u 2 = 242,40   k J / k g h 2 = 263,46   k J / k g

Passo 2

Com o volume específico e a massa podemos calcular o volume do pistão:

V 1 = v 1 ⋅ m 1 = 2   k g ⋅ 0,032659 m 3 k g ⇒ V 1 = 0,06 5318   m 3

V 2 = v 2 ⋅ m 2 = 1   k g ⋅ 0,0 42155 m 3 k g ⇒ V 1 = 0,042155   m 3

O trabalho se inicia quando a pressão atinge 500   k P a . Sabemos que o trabalho a pressão constante é calculado por:

W p i s t a o = P ⋅ Δ V

W p i s t a o = 500   k P a ⋅ 0 , 065318 - 0 , 042155 m 3

W p i s t a o = 11,5815   k J

Passo 3

Vamos calcular também as propriedades do fluxo de saída.

A massa de saída é:

m f l u x o = m 1 - m 2 = 2 - 1 ⇒ m f l u x o = 1   k g

E a entalpia pode ser estimada como a média entre o estado (1) e (2)

h f l u x o = 1 2 h 1 + h 2 = 1 2 316,97 + 263,46   k J k g

h f l u x o = 290,215 k J k g

Passo 4

Vamos aplicar a primeira lei da termodinâmica:

Δ E = E e n t r a - E s a i

Bem, observe que a variação de energia Δ E corresponde a variação de energia interna do sistema. A energia que entra é o trabalho realizado pelo pistão; a energia que sai é o calor e o fluxo de massa:

m 2 ⋅ u 2 - m 1 u 1 = W p i s t a o - Q - m f l u x o h f l u x o

Q = W p i s t a o - m 1 - m 2 h f l u x o + m 1 u 1 - m 2 ⋅ u 2

Aplicando:

Q = 11,5815   k J - 1   k g ⋅ 290,215 k J k g + 2 ⋅ 290,84 k J k g - 1 ⋅ 242,40 k J k g

Q = 60,67   k J

Resposta

  1. W p i s t a o = 11,5815   k J
  2. Q = 60,67   k J
Ver Outros Exercícios desse livro