Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 15.Problemas - Ex. 115
Uma caldeira a vapor aquece água líquida a 200 °C até vapor superaquecido a 4 MPa e 400 °C. Combustível metano (CH4) é queimado à pressão atmosférica com 50% de excesso de ar. O combustível e o ar entram na caldeira a 25 °C, e os produtos de combustão saem a 227 °C. Calcule (a) a quantidade de vapor gerado por unidade de massa de combustível queimado, (b) a mudança na exergia das correntes de combustão, em kJ/kg de combustível, (c) a mudança da exergia da corrente de vapor, em kJ/kg de vapor, e (d) o potencial de trabalho perdido, em kJ/kg de combustível. Considere 
Passo 1
Entendendo o problema:
O processo deste problema consiste na combustão do metano (
. A massa molar do metano e do ar são respectivamente 16kg/mol e 29kg/mol, obtidas da Tabela A-1 do livro.
A equação balanceada para a combustão de 1kmol de metano, contabilizando o excesso de ar, é dada por:
observe que a equação contabiliza a presença de 
livre nos produtos, advinda do fato de que a combustão ocorre com ar em excesso. O balanço de energia para o processo, considerando que não há interação por trabalho (W=0) é dado por:
(1)
Item a:
A figura 1 mostra a tabela de valores e entalpia de formação dos compostos, além dos valores de entalpia nas temperaturas de entrada e saída de combustão. Utilizando a equação (1) e a tabela da Figura 1, temos:
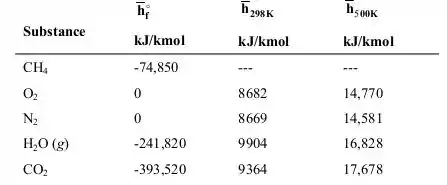
Figura 1: valores e entalpia de formação dos compostos, além dos valores de entalpia nas temperaturas de entrada e saída de combustão.
Assim, o calor gerado por massa de combustível é dado por:
de posse da diferença de entalpia entre a água líquida inicialmente na caldeira e o vapor superaquecido após o processo de aquecido, obtidos das Tabelas A-4 E A-6, a quantidade de vapor obtida por quantidade de combustível é dada por:
Passo 2
Item b:
A geração de entropia do processo é dada pela expressão:
(2)
O ar de entrada está a 1 atm, bem como os gases dos produtos, com pressão total de 1 atm. As entropias devem ser calculadas para cada um dos gases dos produtos, cujas pressões parciais são determinadas através do produto da pressão total pela sua fração molar (
). Então a entropia de cada componente dos produtos é dada pela expressão:
(3)
Figura 2: Dados para o cálculo da entropia de produtos e reagentes
Usando a equação (3) e os dados da tabela da FIgura 2, podemos calcular a soma das entropias dos produtos e reagentes e aplicar na equação (2):
A mudança da exergia dos vapores de combustão é igual a exergia de destruição, pois não há interações por trabalho. Assim:
A troca de exergia por unidade de massa do combustível é portanto:
observando que a troca de exergia é negativa, uma vez que a exergia dos gases de combustão diminui.
Passo 3
item c:
A troca de exergia do sistema é dada pela variação da entalpia subtraída do produto da temperatura pela variação de entropia:
item d:
O potencial de trabalho perdido é o oposto em sinal da variação total de exergia de ambos os sistemas, a câmara de combustão e o conteúdo da caldeira. Assim
Resposta
Respostas: (a) 18,72 kg de vapor/kg de combustível;
(b) 49.490 kJ/kg de combustível; (c) 1.039 kJ/kg de vapor;
(d) 30.040 kJ/kg de combustível