Uma câmara bem isolada, cujo volume é de 1 ft³ (0,003 m³), é mostrada na figura abaixo. Inicialmente a câmara contém ar a 14,7lbf/in² (101,3 kPa) e 100°F (37,8°C). Tubos de alimentação e descarga encontram-se conectados à câmara e têm válvulas que controlam os fluxos de massa na entrada e na saída da câmara. O ar de alimentação encontra-se a 30 lbf/in² (206,8 kPa), 200°F (93,3°C). As válvulas são abertas simultaneamente, permitindo que o ar escoe a uma vazão mássica através de cada válvula. O ar no interior da câmara é bem misturado, de modo que a temperatura e a pressão em cada tempo possam ser consideradas uniformes no todo. Abandonando os efeitos das energias cinética e potencial e usando o modelo de gás ideal com calores específicos constantes para o ar, esboce graficamente a temperatura, em °F, e a pressão, em lbf/in², do ar na câmara versus o tempo para = 1, 2 e 5 lb/min (0,008, 0,01 e 0,04 kg/s).

Vamos começar fazendo o balanço de massa! Como o volume de controle tem apenas 1 saída e nenhuma entrada, temos:

E como a quantidade de ar que entra é igual a que sai, , ou seja:

Fazemos agora o balanço energético, lembrando sempre da hipótese 1!!

Como o processo ocorre lentamente, ou seja, em regime permanente, o estado do ar no tanque em qualquer momento é unifome! Então , e pela hipótese 2, . Substituindo ambas equação no balanço energético, vamos ter:

Lembra que h(t)=.T(t)? Rearrumando um pouco, temos:

Você lembra qual a relação da energia interna específica com a temperatura? Se não lembra não tem problema, é essa aqui:

Que podemos arrumar da seguinte maneira:

Onde

Opa!!! Calma! Encontramos uma EDO aqui! Caso não lembre como resolver, dá uma revisadinha só nessa parte!

Temos que a solução dessa EDO vai ser nesse formato:

Quando t=0, temos T(0) = , logo c = !!!

Substituindo para a forma final da equação:

Beleza!!! Mas não temos nenhuma informação sobre a massa m né? E agora?

Lembra que

Substituindo os dados, temos:

Então:

Que beleza! Esse passo foi tranquilo né?

Já temos a equação da temperatura em razão do tempo, certo?

A gente acha esse k na tabela A-20E!!! Para , temos k=1,4!

Substituindo todos os dados que temos na equação da temperatura, com temperaturas em °F, vamos ficar com:

Agora vamos achar também a equação da pressão em função do tempo p(t):

Pela lei dos gases ideais temos:

Ou seja, substituindo T(t) e os dados:

Tá feio né? Mas vamos lá! Falta só mais um passo

O enunciado nos deu 3 vazões mássicas. Vamos começar pela primeira,

Para essa vazão a equação da temperatura fica:

Já a da pressão fica:

Para a segunda vazão massica,

Temos as equações:

E por fim, para a terceira vazão mássica,

Por fim, temos os gráficos esboçados:

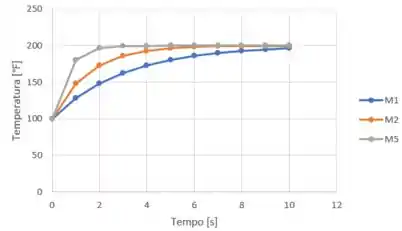
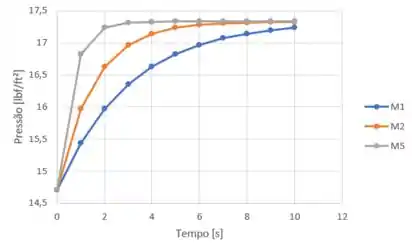
Aqui terminamos!!! Finalmente! Vamos para a próxima?