Um ciclo de refrigeração por compressão de vapor ideal opera em regime permanente usando Refrigerante 134a como fluido de trabalho. Vapor saturado entra no compressor a 2 bar e líquido saturado deixa o condensador a 8 bar. A vazão mássica do refrigerante é 7 kg/min. Determine
(a) a potência do compressor, em kW.
(b) a capacidade frigorífica, em TR.
(c) o coeficiente de desempenho.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
É dado que:
- Vapor saturado entrando no compressor a pressão:
- Líquido saturado saindo do condensador a pressão:
- Taxa de vazão mássica do refrigerante:
O diagrama é mostrado abaixo
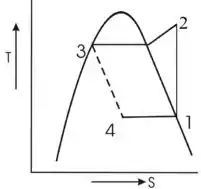
Passo 3
Com das Tabelas saturadas de R-134a
Passo 4
Já que o processo 1-2 é isentrópico,
Com e das tabelas de R-134a superaquecidos. Por interpolação:
Passo 5
No estado 3, o refrigerante está na região líquida saturada. Com pressão das tabelas saturadas, temos
O processo 3-2 está no processo de estrangulamento, então a entalpia é constante
Passo 6
a) A potência do compressor
Passo 7
b) A capacidade de refrigeração
Passo 8
c) O coeficiente de performance
Resposta
a)
b)
c)