Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 11.Problemas - Ex. 124
Um ciclo de refrigeração, que utiliza como fluido de trabalho, opera numa condição onde a temperatura mínima é e a pressão máxima é . A temperatura do refrigerante na seção de saída do compressor é . Admitindo que não existe perda de carga nos escoamentos de nos trocadores de calor e que o compressor é adiabático, determine as transferências de calor específicas no condensador e no evaporador, a eficiência isoentrópica do compressor e o coeficiente de eficácia do ciclo.
Passo 1
Oi galera, como vocês estão? Espero que bem, vamos resolver mais essa! Bem, antes de tudo iremos observar o diagrama abaixo, que representa a situação descrita no Enunciado:
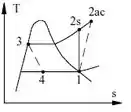
De acordo com o diagrama e o que foi apresentado no enunciado, temos que , e , obteremos os dados das propriedades utilizando a Tabela . Usaremos as seguintes equações:
(1)
(2)
(3)
(4)
Dito isto, vamos pra o problema!
Passo 2
Primeiramente, vamos determinar cada uma das propriedades, estado por estado!
Estado (1): Interno ao compressor, vapor de saturação de , , ;
Estado (2): Saída atual do compressor, ;
Estado (2s): Outro estado do compressor, , ; ,
Estado (3): Saída do condensador, saturação do liquido a , ;
Estado (4): Válvula de saída, ;
Com os dados estabelecidos, agora passaremos para a aplicação das equações!
Passo 3
Começaremos pela equação (1):
Agora para a equação (2):
Agora precisaremos calcular e :
Com esses dois termos devidamente prontos, podemos ir para as equações que restam, começando pela de número (3):
Agora para a equação (4):
Questão resolvida! até a próxima, fiquem bem e bye bye.