Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 81
Um ciclo Stirling padrão a ar opera com uma pressão máxima de e uma pressão mínima de . O volume máximo é vezes o volume mínimo, e o reservatório a baixa temperatura está a . Considerando uma diferença de temperatura de entre os reservatórios externos e o ar, quando for aplicável, calcule o calor específico adicionado ao ciclo e o seu trabalho específico líquido.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Se você não está familiarizado com o ciclo Stirling, observe abaixo o seu diagrama .
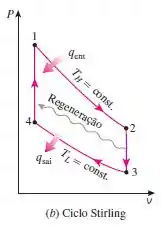
Como devemos considerar calores específicos constantes à temperatura ambiente, temos que:
A partir do diagrama, sabemos que o volume máximo é o dos estados e . O volume mínimo é o usado no estado e . Ou seja:
Passo 2
Analisando o processo temos que:
Substituindo os valores do enunciado, temos que:
Passo 3
O processo acontece a volume constante, logo:
Substituindo os valores, temos que:
Para o calor fornecido no processo , temos que:
Substituindo os valores, temos que:
Passo 4
Para o calor fornecido no processo , temos que:
Substituindo os valores, temos que:
O trabalho líquido será: