Conforme ilustrado na Fig. P3.129, um dos lados de um reservatório rígido e isolado mantém 2 m3 de ar inicialmente a 27°C e 0,3 MPa. Uma fina membrana separa o ar de um espaço evacuado com 3 m3 de volume. Devido à pressão do ar a membrana estica e finalmente se rompe, permitindo que o ar ocupe todo o volume. Admitindo o modelo de gás ideal para o ar, determine (a) a massa do ar, em kg, (b) a temperatura final do ar, em K, e (c) a pressão final do ar, em MPa.
Passo 1
Ooopa, beleza?
Vamos lá pra mais uma questão bem interessante de termodinâmica!
Passo 2
É dado que:
- Volume inicial:
- Temperatura inicial:
- Pressão inicial:
- Volume inicial evacuado:
O esquemático é dado por
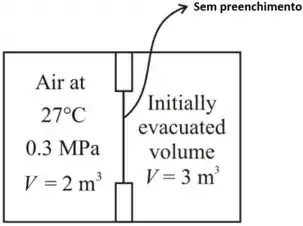
Passo 3
a) massa de ar
Passo 4
b) Usando a primeira lei da termodinâmica
Como o sistema é isolado e não há movimento na fronteira então
Passo 5
c) Como a temperatura permanece constante
Resposta
a)
b)
c)