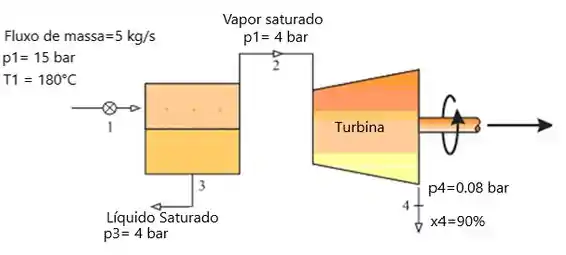
Conforme mostrado na Fig. P4.105, água quente de resíduos industriais a 15 bar, 180°C e com uma vazão mássica de 5 kg/s entra em um separador através de uma válvula. Líquido saturado e vapor saturado saem do separador em fluxos distintos, cada um a 4 bar. O Vapor saturado entra na turbina e se expande até 0,08 bar e . As perdas de calor e os efeitos das energias cinética e potencial podem ser ignorados. Para a operação em regime permanente, determine a potência, em hp, desenvolvida pela turbina.

Pela equação de equilíbrio da taxa de energia

O trabalho realizado, transferência de calor, energia cinética e potencial são insignificantes.

Considerando os seguintes valores da entalpia específica e da temperatura de saturação para água residual industrial quentes correspondente a 15 bar e 180 °C da Tabela A-3, “Propriedades da água saturada” como segue:

Calculando a entalpia no estado 1, usando a seguinte expressão

Considerando as propriedades do vapor da tabela A-3 “Propriedades de água saturada”, seguimos

Fazendo as substituições na equação (1)

Portanto, a taxa de fluxo de massa na saída 2 é de

Considere o balanço de energia da turbina em estado estacionário da seguinte forma

Negligencie as mudanças de energia cinética, potencial , a equação de energia, a transferência de calor

Considere as seguintes propriedades da tabela A-3 “Propriedades da água saturada”

Fazendo substituições na equação (2)

Portanto, a potência desenvolvida pela turbina é de