Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 17.Problemas - Ex. 105
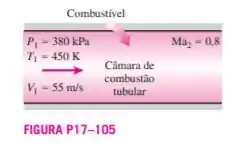
Considere uma câmara de combustão tubular com de diâmetro. O ar entra no tubo a . O combustível com poder calorífico de é queimado com ar. Considerando que o número de Mach na saída é , determine a taxa de queima do combustível e a temperatura de saída. Considere uma combustão completa e despreze o aumento da vazão mássica devido à massa do combustível.
Passo 1
Para resolvermos esse problema vamos assumir, primeiramente, que as suposições associadas ao fluxo de Rayleigh são válidas, além do que a combustão completa é tratado como um processo de adição de calor, sem alteração na composição química do fluxo e, por fim, o aumento de vazão mássica devido à injeção de combustível é desconsiderada. Temos ainda algumas constantes que nos serão de grande valia aqui
Passo 2
Pois bem, dando prosseguimento a resolução vamos ter a densidade de entrada e a vazão mássica do ar serão dadas por
Dessa forma poderemos encontrar que a temperatura de estagnação e o número Mach na entrada são
Passo 3
Temos que as funções de fluxo Rayleigh correspondentes aos números Mach de entrada e saída podem ser encontrados na usando funções analíticas vamos ter
Sendo assim, vamos ter que a temperatura de saída, a temperatura de estagnação e a velocidade são determinadas como
Então, a vazão mássica do combustível é determinada como sendo