Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 74
Considere um ciclo Ericsson ideal com ar como fluido de trabalho executado em um sistema com escoamento em regime permanente. O ar está a e no início do processo de compressão isotérmica, durante o qual de calor são rejeitados. A transferência de calor para o ar ocorre a . Determine (a) a pressão máxima do ciclo, (b) o trabalho líquido produzido por unidade de massa de ar e (c) a eficiência térmica do ciclo.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O exercício nos pede para considerar um ciclo Ericsson ideal com ar como fluido de trabalho. Nos diz também para considerar o sistema com escoamento em regime permanente.
Se você não está familiarizado com o ciclo Ericsson, observe abaixo o seu diagrama .
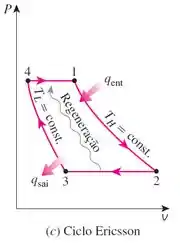
Nos é dito que o ar está a e no início do processo de compressão isotérmica, durante o qual de calor são rejeitados. Como podemos observar no diagrama, a compressão isotérmica ocorre no processo , portanto:
Como devemos considerar calores específicos constantes à temperatura ambiente, temos que:
Passo 2
Depois dessa introdução básica ao enunciado, podemos traçar as estratégias para resolver os itens. O item “a” nos pede a pressão máxima do ciclo.
Sabendo que a pressão é máxima na saída do compressor, ou seja, no estado .
Bom... Sabemos que em um processo isotérmico, a transferência de calor está relacionada com a variação de entropia:
Portanto, analisando o processo de compressão, temos que:
Aplicando ao nosso exercício, temos que:
Sabemos também que a variação de entropia de um gás ideal durante um processo isotérmico é dada por:
Aplicando ao exercício, temos que:
Logo:
A pressão máxima será:
Passo 3
O item “b” nos pede o trabalho líquido específico. Sabemos que:
Para um ciclo reversível ideal, temos que:
Portanto:
Substituindo os valores, temos que:
Logo:
O trabalho será então:
Passo 4
Para resolver o item “c” é só aplicar a definição de eficiência térmica para um ciclo ideal:
Ou: