Considere um ciclo de refrigeração Brayton com um trocador de calor regenerativo. O ar entra no compressor a 500°R (4,6°C) e 16 lbf/in2 (110,3 kPa), e é comprimido isentropicamente até 45 lbf/in2 (310,3 kPa). O ar comprimido entra no trocador de calor regenerativo a 550°R (32,4°C) e é resfriado até 490°R (–0,9°C) antes de entrar na turbina. A expansão pela turbina é isentrópica. Se a capacidade frigorífica for de 14 TR (49,2 kW), calcule
(a) a vazão volumétrica na entrada do compressor, em ft3/min.
(b) o coeficiente de desempenho.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
É dado que:
- Temperatura na entrada do compressor:
- Pressão na entrada do compressor:
- Pressão na saída do compressor:
- Temperatura na entrada do trocador de calor:
- Temperatura na entrada da turbina:
- Capacidade de refrigeração:
O diagrama é mostrado
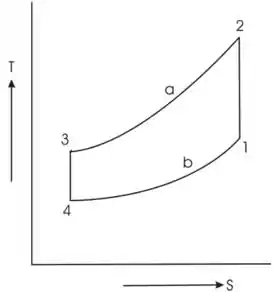
Passo 3
Da tabela de propriedades do ar a
O processo 1-2 é isentrópico, usando a relação isentrópica
Da tabela de propriedades do ar com , interpolando
Passo 4
Da tabela de propriedades do ar a
O processo 3-4 é isentrópico, usando a relação isentrópica
Da tabela de propriedades do ar com , interpolando
Da tabela de propriedades do ar com
Passo 5
Aplicando o balanço de energia na equação do trocador de calor
Sabemos que a capacidade de refrigeração é
Passo 6
a) usando a equação do gás ideal a taxa de razão volumétrica na entrada do compressor é
Passo 7
b) o coeficiente de performance é
Resposta
a)
b)