Considere um ciclo de refrigeração a vapor de Carnot com o Refrigerante R134a como fluido de trabalho. O ciclo mantém uma região fria a 40°F (4,4°C) quando a temperatura ambiente é de 90°F (32,2°C). Dados dos estados principais do ciclo são apresentados na tabela a seguir. Os estados estão indicados conforme a Fig. 10.1. Esboce o diagrama T–s para o ciclo e determine
(a) a temperatura no evaporador e no condensador, ambas em °R.
(b) a potência do compressor e da turbina, ambas em Btu por lb de refrigerante.
(c) o coeficiente de desempenho
(d) o coeficiente de desempenho para um ciclo de Carnot operando nas temperaturas dos reservatórios.
Compare os coeficientes de desempenho determinados em (c) e (d), e comente.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
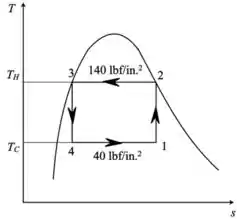
O diagrama para o ciclo de refrigeração de Carnot
Passo 3
a) Obtendo as propriedades do R134a da Tabela A-11E “Propriedades de Refrigerante 134a Saturado: Tabela de Pressão” em
- Entalpia específica de vapor saturado:
- Temperatura de saturação:
- Entalpia específica de vapor saturado:
- Temperatura de saturação:
Como o valor de , o refrigerante está em uma região bifásica e a temperatura de evaporação é igual a temperatura saturada.
Passo 4
Obtendo as propriedades do R134a da Tabela A-11E “Propriedades de Refrigerante 134a Saturado: Tabela de Pressão” em
Como o valor de , o refrigerante está no estado de vapor região bifásica e a temperatura de condensação é igual a temperatura saturada.
Passo 4
b) Calculando o trabalho de entrada do compressor
Calculando o trabalho de saída da turbina
Passo 5
c) calculando o coeficiente de performance do ciclo
Passo 6
d) Calculando o coeficiente de performance para o ciclo de Carnot operando na temperatura dos reservatórios (lembrando de converter as temperaturas para a escala Rankine)
Passo 7
Dos resultados obtidos, notamos que o COPE do ciclo de Carnot é maior que o COP do sistema atual. Isso é por que a temperatura do evaporador e do condensador devem ter alguma diferença devido a transferência de calor com a vizinhança. Essa mudança na temperatura reduz o COP do sistema.
Resposta
a)
b) e
c)
d)