Considere um ciclo Stirling ideal que usa ar como fluido de trabalho. O ar está a 350 K e 200 kPa no início do processo de compressão isotérmica, e 900 kJ/kg de calor são fornecidos para o ar de uma fonte a 1.800 K. Determine

1. a pressão máxima do ciclo
2. o trabalho líquido por unidade de massa de ar.

Vamos assumir que:

As premissas do padrão aéreo são aplicáveis.

As alterações cinéticas e potenciais de energia são insignificantes.

O ar é um gás ideal com aquecimentos específicos constantes.

Sabemos que as propriedades do ar à temperatura ambiente são:

Vamos observar a figura:

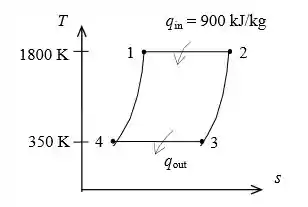
A alteração da entropia durante o processo 1-2 é:

Então, para a pressão máxima do ciclo: