Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 178

Considere um ciclo de turbina a gás ideal com um estágio de compressão e dois estágios de expansão e regeneração. A razão de pressão em cada estágio da turbina é a mesma. O gás de exaustão da turbina de alta pressão entra no regenerador e depois entra na turbina de baixa pressão para expandir-se até a pressão de entrada no compressor. Determine a eficiência térmica desse ciclo em função da razão de pressão do compressor e da razão entre as temperaturas de entrada na turbina de alta pressão e no compressor. Compare seus resultados com a eficiência do ciclo-padrão com regeneração.

Passo 1

O diagrama T-s do ciclo é como mostrado na figura.

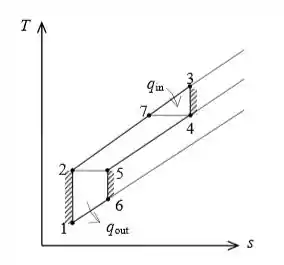
Se a taxa de pressão geral do ciclo for r p , que é a taxa de pressão no compressor, a taxa de pressão em cada estágio da turbina, no caso ideal, se torna r p . Usando as relações isentrópicas, as temperaturas na saída do compressor e da turbina podem ser expressas como:

T 5 = T 2 = T 1 P 2 P 1 ( k - 1 ) / k = T 1 ( r p ) ( k - 1 ) / k

T 7 = T 4 = T 3 P 4 P 3 ( k - 1 ) / k = T 2 r p ( 1 - k ) / 2 k

T 6 = T 5 P 6 P 5 ( k - 1 ) / k = T 5 1 r p ( k - 1 ) / k = T 2 r p ( 1 - k ) / 2 k = T 1 r p ( 1 - k ) / k r p ( 1 - k ) / 2 k = T 1 r p ( 1 - k ) / 2 k

Passo 2

Então,

q i n = h 3 - h 7 = c p ( T 3 - T 7 ) = c p T 3 ( 1 - r p ( 1 - k ) / 2 k )

q o u t = h 6 - h 1 = c p ( T 6 - T 1 ) = c p T 1 ( r p ( k - 1 ) / 2 k - 1 )

e

η t h = 1 - q o u t q i n = 1 - c p T 1 r p ( k - 1 ) / 2 k - 1 c p T 3 1 - r p ( 1 - k ) / 2 k = 1 - T 1 T 3 r p ( k - 1 ) / 2 k

E então, a eficiência térmica do ciclo regenerativo ideal de estágio único é dada como:

η t h = 1 - T 1 T 3 r p ( k - 1 ) / k

Portanto, o ciclo regenerativo com dois estágios de expansão tem uma eficiência térmica mais alta que o ciclo regenerativo padrão com um único estágio de expansão para qualquer valor dado da razão de pressão r p .

Resposta

η t h = 1 - T 1 T 3 r p ( k - 1 ) / k

Portanto, o ciclo regenerativo com dois estágios de expansão tem uma eficiência térmica mais alta que o ciclo regenerativo padrão com um único estágio de expansão para qualquer valor dado da razão de pressão r p .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o rendimento térmico da usina termelétrica a vapor dada no Exemplo 6.8.
Um motor de carro queimou 5 kg de combustível (equivalente a adicionar Q H ) com um rendimento térmico de 28%, rejeitando energia pelo radiador e pela descarga. Considere que o combustível tem um pode
Um motor de automóvel opera com um rendimento térmico de 35%. Considere que o condicionador de ar (refrigerador tem um coeficiente de performance de β = 3 , e que ele resfria o interior do carro usand
Para cada um dos casos no Problema 7.8, determine se a bomba de calor satisfaz a primeira lei (equação de energia) e se viola a segunda lei.
Um condicionador de ar, com potência de entrada de 1,2k W , pode trabalhar como um refrigerador ( β = 3 ) ou como uma bomba de calor ( β ' = 4 ) . O condicionador mantém, durante todo o ano, um escrit