Considere o seguinte ciclo de refrigeração por compressão de vapor que é utilizado para manter uma região fria a uma temperatura TC, enquanto a temperatura ambiente é 80°F (26,7°C): vapor saturado entra no compressor a 15°F (–9,4°C), abaixo de TC, e o compressor opera adiabaticamente com uma eficiência isentrópica de 80%. O líquido saturado sai do condensador a 95°F (35°C). Não existem quedas de pressão no evaporador e no condensador, e a capacidade frigorífica é de 1 TR (3,5 kW). Esboce graficamente a vazão mássica de refrigerante em lb/min, o coeficiente de desempenho e a eficiência de refrigeração, versus TC variando de 40°F (4,4°C) a –25°F (–31,7°C), considerando que o refrigerante é
(b) propano.
A eficiência de refrigeração é definida como a razão entre o coeficiente de desempenho do ciclo e o coeficiente de desempenho de um ciclo de refrigeração de Carnot operando entre reservatórios térmicos que se encontram à temperatura ambiente e à temperatura da região fria.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?! Vamos usar o EES (Engineering Equation Solver) pra ajudar a gente nessa questão beleza?
Passo 2
Desenhando o diagrama mostrando os diferentes processos em compressão de vapor no ciclo de refrigeração
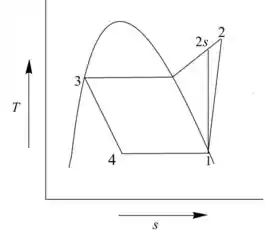
- Processo 1-2: compressão atual
- Processo 2-3: transferência de calor do refrigerante
- Processo 3-4: processo de estrangulamento
- Processo 4-1: transferência de calor para o refrigerante
Passo 3
a) Considerando o Propano
Podemos escrever o seguinte programa no EES
"Dados Iniciais"
T1 = TC - 15 "temperatura da entrada do compressor"
eta_c = 0,8 "eficiência do compressor isentrópico"
T3 = 95 "temperatura de saída do compressor"
Qdotin = 1 "capacidade do refrigerante [ton]"
TC = -25 "temperatura da região de resfriamento"
TH = 80 "temperatura ambiente"
"Cálculos nas Tabelas"
x1 = 1 "vapor saturado entra no compressor"
p1 = Pressure(Propane; T=T1; x=x1)
h1 = Enthalpy(Propane; P=p1; x=x1)
s1 = Entropy(Propane; P=p1; x=x1)
s2s = s1 "o processo 1 a 2s é uma compressão isentrópica"
p2 = p3
s2s = Entropy(Propane; P=p2; T=T2s) "entropia de vapor superaquecido"
h2s = Enthalpy(Propane; P=p2; T=T2s) "entalpia de vapor superaquecido"
h2 = h1 + (h2s - h1)/eta_c "entalpia de vapor superaquecido no estado 2"
p3 = Pressure(Propane; T=T3; x=0)
x3 = 0 "líquido saturado sai do condensador"
h3 = Enthalpy(Propane; P=p3; x=x3) "entalpia saturada no estado 3"
h4 = h3 "entalpia permanece constante no processo de estrangulamento"
mdot = (Qdotin * 200)/(h1 - h4) "taxa de vazão mássica do refrigerante"
beta = (h1 - h4)/(h2 - h1) "coeficiente de performance do ciclo de refrigerante"
betacarnot = (TC + 460)/((TH + 460) - (TC + 460)) "coeficiente de performance do ciclo de Carnot"
eff = beta / betacarnot "eficiência da refrigeração"
Passo 4
Criamos um plot com a vazão mássica, o coeficiente de performance e a eficiência com respeito a temperatura da região de resfriamento.
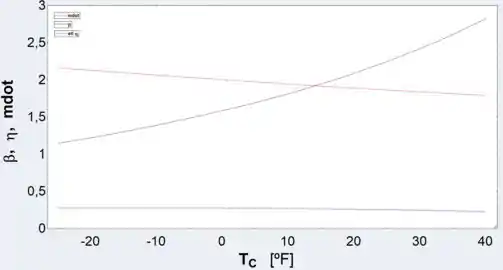
Resposta
Ei, a resposta está no passo a passo :)