Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 1.Problemas - Ex. 77

Considere um tubo em U cujas extremidades estão abertas para a atmosfera. Coloca-se agua em uma das colunas do tubo em U, e óleo leve ( ρ = 790   k g / m 3 ) na outra. Uma coluna contem agua a 70   c m de altura, enquanto a outra contem ambos os fluidos com uma razão entre as alturas de óleo e de agua igual a 4. Determine a altura de cada fluido nessa coluna.

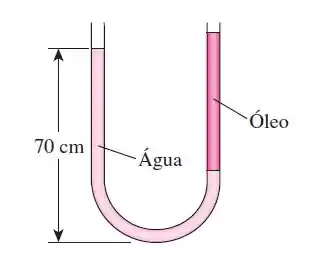
Passo 1

Para determinar a colunas, vamos ilustrar primeiro:

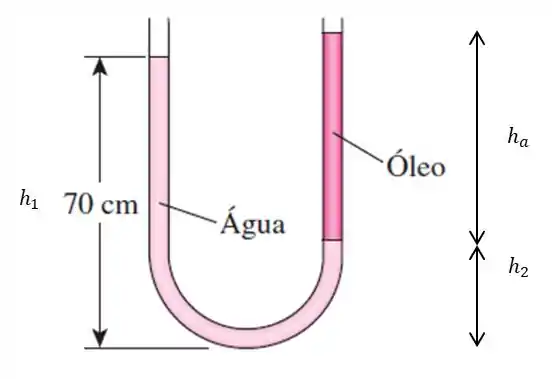
Certo possuímos h 1 e h 2 que pertencem ao fluido água e h a ao óleo.

Considerando a densidade do óleo ρ ó l e o = 790   k g / m 3   e da água ρ á g u a = 1000   k g / m 3 .

E notando a relação entre as alturas que foram ditas no enunciado:

h a h 2 = 4

Passo 2

Agora escolheremos dois pontos no mesmo fluido para aplicarmos o princípio de Pascal:

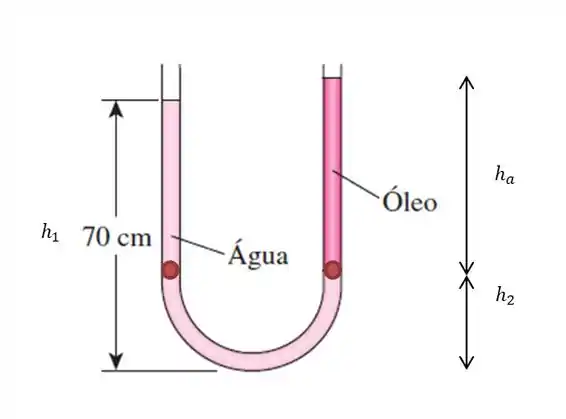
Do lado esquerdo temos:

P = P a t m + ρ á g u a g h 1

E do lado direito:

P = P a t m + ρ á g u a g h 2 + ρ ó l e o g h a

Segundo princípio de Pascal podemos igualar esta duas equações:

P a t m + ρ á g u a g h 1 = P a t m + ρ á g u a g h 2 + ρ ó l e o g h a

Isolando h 1 e simplificando oque é possível:

h 1 = h 2 + ρ ó l e o ρ á g u a h a

Para dar continuidade no calculo utilizaremos relação das alturas dita anteriormente:

Resolvendo para h 2 :

h a = 4 h 2

h 1 = h 2 + ρ ó l e o ρ á g u a h a

h 1 = h 2 + ρ ó l e o ρ á g u a 4 h 2

0,7 = h 2 + 790 1000 4 h 2

h 2 = 0,168   m

Resolvendo para h a :

h 1 = h 2 + ρ ó l e o ρ á g u a h a

h 1 = h a 4 + ρ ó l e o ρ á g u a h a

0,7 = h a 4 + 790 1000 h a

h a = 0,673   m

Resposta

h a = 0,673   m

h 2 = 0,168   m

Ver Outros Exercícios desse livro