Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 39
Considere uma usina de potência a vapor que opera em um ciclo de Rankine ideal com reaquecimento. A usina mantém a caldeira a 7.000 kPa, o ponto de reaquecimento a 800 kPa e o condensador a 10 kPa. O título da mistura na saída de ambas as turbinas é de 93%. Determine a temperatura na entrada de cada turbina e a eficiência térmica do ciclo.
Passo 1
Oi pessoal, tudo bem?
Consideremos o esboço para este problema:
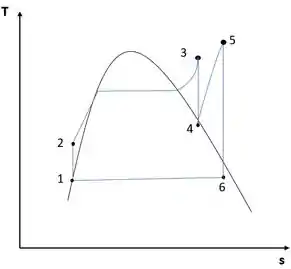
Bem, para início de análise, o problema indica que o estado 1 encontra-se em líquido saturado. Sabemos que o estado 1 encontra-se à mesma pressão do estado 6. Então, utilizando o auxílio das tabelas A.4, A.5 e A6, é possível encontrar algumas relações termodinâmicas.
Passo 2
Temos a pressão de , na tabela de líquido saturado, podemos obter:
Sabendo que o trabalho específico pode ser dado por :
Passo 3
O estado 3 está em vapor superaquecido com porém não sabemos ainda a sua temperatura ou entropia.
Mas sabemos que e o título é , portanto, das tabelas:
Para encontrar o :
Então, como , então:
O estado 5 está em vapor superaquecido com porém não sabemos ainda a sua temperatura ou entropia.
Mas sabemos que e o título é , portanto, das tabelas:
Para encontrar o :
Então, como , então:
Passo 4
Então, o calor que entra é:
O trabalho da turbina é:
Assim, a eficiência térmica é:
Resposta
Portanto: ;