Demonstre que a escala de temperatura de gás (Seção 5.8.2) idêntica à escala de temperatura de Kelvin (Seção 5.8.1).

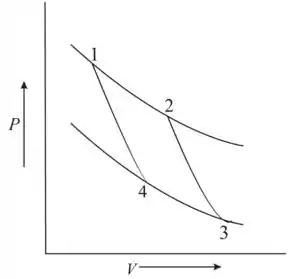
Considerando a potência do ciclo de Carnot operando entre dois reservatórios térmicos de energia e o ciclo consiste de

• Processo 1-2 é uma expansão isotérmica a temperatura
• Processo 2-3 é uma expansão adiabática
• Processo 3-4 é uma compressão isotérmica a
• Processo 4-1 é uma compressão adiabática

Considerando o processo 1-2:

Escrevendo a equação para a transferência de trabalho durante o processo 1-2

Escrevendo a primeira lei da Termodinâmica

Substituindo para

A temperatura é constante durante o processo isotérmico. Substituindo por

Substituindo para

Considerando o processo 1-2:

Já que os processos 2-3 e 4-1 são processos adiabáticos, a transferência de calor durante esses processos é zero

Considerando o processo 2-3:

Escrevendo a primeira lei da termodinâmica

Considerando o processo 4-1:

Escrevendo a primeira lei da termodinâmica

Comparando os resultados obtidos nos Passos 7 e 8, temos

Considerando o processo 3-4

Escrevendo a equação para a transferência de trabalho

Escrevendo a primeira lei da termodinâmica

A temperatura é constante durante um processo isotérmico

Dividindo as equações obtidas

Substituindo

Essa equação corresponde a seguinte equação

Isso significa que , onde é a temperatura na escala Kelvin. Então concluímos que a temperatura no gás é idêntica a temperatura na escala Kelvin.