Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 2.Problemas - Ex. 69
Em um determinado local, o vento sora a uma velocidade constante de 7 m/s. Determine a energia mecânica do ar por unidade de massa e o potencial para geração de potência de uma turbina eólica com pás de 80 m de diâmetro naquele local. Determine também a geração real de potência elétrica, considerando uma eficiência global de 30%. Suponha que a densidade do ar seja de 1,25 kg/.
Passo 1
Temos uma turbina eólica como representada no esquema a seguir:
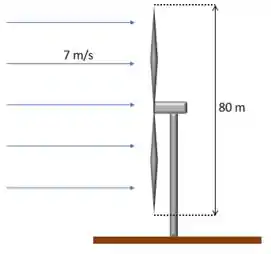
Temos que a única energia mecânica atuando no sistema é a energia cinética do vento, sabemos que a energia cinética por unidade de massa é dada por:
Passo 2
Vamos considerar que toda a energia cinética será convertida em trabalho, daí, com um fluxo de mássico de ar movimentando as pás da turbina, teremos uma potência derivada do trabalho da energia cinética.
Para descobrirmos o fluxo mássico de arque passa pelas pás das turbinas, temos:
A área de contato do ar com as pás será da seguinte forma:
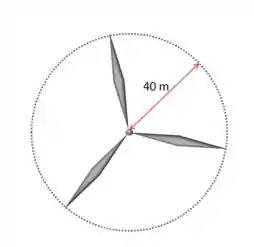
Teremos um círculo, cuja área é dada por , assim:
Passo 3
Assim, a potência da turbina é dada por:
Passo 4
A geração real de potência elétrica considerando a eficiência de 30% é:
Resposta
A energia mecânica do ar por unidade de massa é de 0,0245 kJ/kg e a geração de potência da turbina é de 1077,02 kW. A geração real de potência elétrica da turbina considerando a eficiência de 30% é de 323,1 kW.