Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 9.Problemas - Ex. 13

Determine a constante elástica equivalente e a massa equivalente do sistema mostrado na Figura 1.65 com relação a θ . Admita que as barras AOB e CD sejam rígidas com massa desprezível.

Passo 1

Saalve, tudo certo? Bora pra questão! Para facilitar nosso entendimento sobre a questão, a gente faz esse esqueminha pra entender todas as simplificações que a gente vai fazer ao longo das questões.

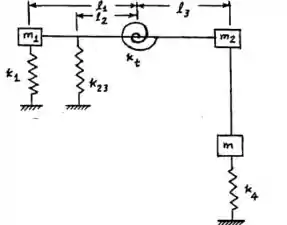
Temos que:

k 23 = k 2 k 3 k 2 + k 3

k 4 = A q g = π d 2 4 q g

Da energia cinética,

1 2 m 1 l 1 θ 2 + 1 2 m 2 + m l 3 θ 2 = 1 2 J e q θ 2

Para

Passo 2

Da energia potencial,

1 2 k 1 l 1 θ 2 + 1 2 k 23 l 2 θ 2 + 1 2 k t θ 2 + 1 2 k 4 l 3 θ 2 = 1 2 k e q θ 2

Portanto:

J e q = m 1 l 1 2 + m 2 + m l 3 2 ;

k e q = k 1 l 1 2 + k 23 l 2 2 + k t + k 4 l 3 2

Resposta

J e q = m 1 l 1 2 + m 2 + m l 3 2 ;

k e q = k 1 l 1 2 + k 23 l 2 2 + k t + k 4 l 3 2

Ver Outros Exercícios desse livro