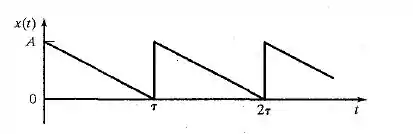
Determine a expansão por série de Fourier da função periódica mostrada nas Figura 1.92. Além disso, represente em gráfico o espectro de frequência correspondente.
Passo 1
Faaala pessoal, como vocês tão? Bora pra mais uma questãozinha comigo!
Dessa figura indicada no enunciado, nós temos, com variando de :
Começaremos tratando dos componentes de uma série de Fourier de cossenos (:
Uma vez demonstrado isso, vamos trabalhar com o outro componente de cossenos:
Passo 2
Agora que já tratamos dos componentes de cossenos, trataremos no componente de seno:
Por fim, tendo tratado de todas as componentes, chegamos à conclusão que: