Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 4.Problemas - Ex. 46
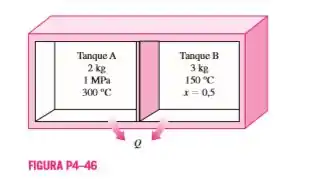
Dois tanques (tanque A e tanque B) são separados por uma partição. Inicialmente, o tanque A contém 2 kg de vapor a 1 MPa e 300 °C, enquanto o tanque B contém 3 kg de uma mistura saturada de líquido e vapor com a fração em massa de vapor igual a 50%. A partição é então removida e os dois lados se misturam até que seja estabelecido o equilíbrio mecânico e térmico. Considerando que a pressão no estado final é de 300 kPa, determine (a) a temperatura e o título do vapor (se houver mistura) no estado final e (b) a perda de calor dos tanques.
Passo 1
Inicialmente vamos consultar as tabelas de vapor para obter informações sobre as propriedades iniciais em cada tanque, assim:
Quando os tanques se misturam, teremos que o volume total será a soma dos volumes parciais e a massa total a soma das massas totais, assim:
Daí, conseguimos encontrar o volume específico no estado final do processo, ou seja, após os tanques se juntarem, assim:
Analisando as tabelas de vapor para a pressão final de e volume específico de , encontraremos que a sua temperatura será de e seu título pode ser obtido da seguinte forma:
Assim, teremos que a energia interna ao final do processo será de:
Passo 2
Temos que o balanço de energia para um sistema fechado pode ser dado por:
Considerando os dois tanques como sistema, poderemos considerar que as variações das energias cinética e potencial são desprezíveis, além de que o trabalho será nulo, assim:
O sinal negativo refere-se ao calor que está saindo dos tanques, que está sendo transferido para as vizinhanças.
Resposta
Ei, a resposta está no passo a passo :)