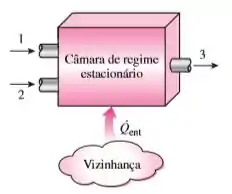
Duas correntes de massa de dois diferentes gases ideais são misturadas em uma câmara com escoamento em regime permanente, que ao mesmo tempo recebe energia por transferência de calor das vizinhanças. O processo de mistura ocorre a uma pressão constante sem trabalho, e as energias cinética e potencial possuem variações desprezíveis. Considere que os gases têm calores específicos constantes.
(a) Determine a expressão para a temperatura final da mistura, utilizando a taxa de transferência de calor para a câmara de mistura e as vazões mássicas, os calores específicos e as temperaturas das três correntes de massa.
(b) Obtenha uma expressão para a vazão volumétrica de saída, considerando a taxa de transferência de calor para a câmara de mistura, a pressão da mistura, a constante universal dos gases e os calores específicos e as massas molares dos gases de admissão e de saída da mistura.
(c) Para o caso especial de uma mistura adiabática, mostre que a vazão volumétrica de saída é uma função de duas vazões volumétricas de entrada e dos calores específicos e massas molares das entradas e saída.
(d) Para o caso especial de uma mistura adiabática dos mesmos gases ideais, mostre que a vazão volumétrica de saída é uma função das duas vazões volumétricas de entrada.
Passo 1
Dois fluxos de massa de dois gases ideais diferentes são misturados em uma câmara de fluxo constante enquanto recebem energia por transferência de calor do ambiente. Expressões para a temperatura final e o fluxo volumétrico de saída devem ser obtidas e dois casos especiais devem ser avaliados.
(a) Balanços de massa e energia para o processo de mistura:

Passo 2
(b) A expressão para o fluxo de volume de saída é obtida da seguinte forma:

A massa molar da mistura M3 é encontrada da seguinte forma:

Passo 3
(c) Para mistura adiabática o Ql é zero, e o fluxo de volume da mistura torna-se
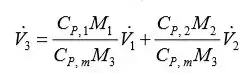
(d) Ao misturar adiabaticamente os mesmos dois gases ideais, o fluxo volumétrico da mistura torna-se

Resposta
Ei, a resposta está no passo a passo :)