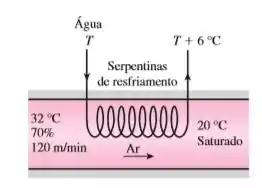
O ar entra a 1 atm, 32 °C e 70% de umidade relativa em uma seção de resfriamento com 40 cm de diâmetro, a uma velocidade de 120 m/min. O ar é resfriado enquanto passa sobre uma serpentina de resfriamento pela qual a água flui. A água passa por uma elevação de temperatura de 6 °C. O ar sai da seção de resfriamento saturado a 20 °C. Determine

1. a taxa de transferência de calor
2. a vazão mássica da água e
3. a velocidade de saída da corrente de ar.

A pressão de saturação da água a 32ºC é de 4,76 kPa (Tabela A-4). Em seguida, a temperatura do ponto de orvalho da corrente de ar a 32 ° C se torna:

como o ar é resfriado a 20 ° C, abaixo da temperatura do ponto de orvalho, parte da umidade do ar se condensará. A quantidade de umidade no ar diminui devido à desumidificação. Os estados de entrada e saída do ar são completamente especificados e a pressão total é de 1 atm. Em seguida, as propriedades do ar em ambos os estados são determinadas a partir do gráfico psicrométrico (Fig. A-31 ou EES) como sendo

E

Então,

Aplicando o balanço de massa de água e as equações de balanço de energia na seção combinada de resfriamento e desumidificação (excluindo a água),

Balanço de Massa de Água:

Equilíbrio energético:

Na letra b, observando que o calor perdido pelo ar é ganho pela água de resfriamento, a taxa de fluxo mássico da água de resfriamento é determinada a partir de

Na letra c, a velocidade de saída é determinada a partir da conservação da massa de ar seco;