A Fig. P1.30 ilustra um gás contido em um conjunto cilindro-pistão pistão vertical. Um eixo vertical, cuja área transversal é de 0,8 cm2 é preso no topo do pistão. Determine a magnitude da força F, em N, que age sobre o eixo, necessária se a pressão do gás for de 3 bar. As massas do pistão e do eixo são 24,5 kg e 0,5 kg, respectivamente. O diâmetro do pistão é de 10 cm. A pressão atmosférica local é 1 bar. Considere que o pistão se move suavemente no cilindro e que g = 9,81 m/s2.

O enunciado nos dá alguns parâmetros:

• Área transversal:
• Pressão:
• Massa do pistão:
• Massa do eixo:
• Diâmetro do pistão:
• Pressão atmosférica:
• Aceleração gravitacional:

Com todos os parâmetros anotados, vamos seguir para os próximos passos.

Bom, o problema está nos pedindo para acharmos a força que está agindo sobre o eixo. Quando estamos falando de forças agindo sobre um corpo, qual a primeira coisa que tem que vir na nossa cabeça pra resolver esse problema?

É isso aí, vamos desenhar um diagrama de corpo livre pro nosso problema pra observarmos melhor o que está acontecendo.

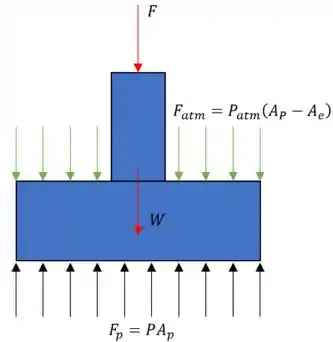
Onde,

• é a força agindo no eixo
• é a força devido a pressão atmosférica (já que )
• é a área do pistão
• é a área do eixo
• é a força devido ao peso
• é força agindo no pistão
• é a pressão
• é a área do pistão.

Considerando o equilíbrio de forças na direção vertical (positivo para cima)

Temos que é o peso total do sistema, ou seja

Temos que uma força aplicada em uma área é dada por , assim podemos substituir

• =

Sabemos também que o peso de um corpo de massa é dado por

Substituindo esses valores na Equação para

Resolvendo para a força

Calculando a área da seção transversal do pistão

Substituindo os valores obtidos na Equação para a força