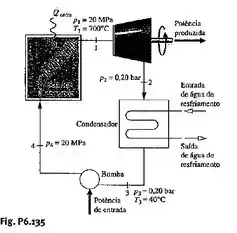
A Fig. P6.135 fornece um esboço de uma planta de potência a vapor operando em regime permanente que utiliza água como fluido de trabalho. Dados localizados em posições estratégicas são fornecidos na figura. O escoamento entre a turbina e a bomba ocorrem isentropicamente. O escoamento entre o gerador de vapor e o condensador ocorrem a pressão constante. As perdas de calor e os efeitos das energias cinética e potencial podem ser desprezados. Esboce os quatro processos em série desse cliclo em um diagrama T-s. Determine a eficiência térmica.
Passo 1
Simbora resolver essa!
Da tabela A-4 conseguimos algumas propriedades do vapor de água, teremos:
Já na tabela A-3, tendo , conseguimos também algumas propriedades, temos:
Show, coletamos uns dados bacanas pra fazer a questão, agora vamo lá!
Passo 2
Show, temos que , pois temos uma expansão isentrópica na turbina, assim:
Com isso, vamos achar o título em 2, logo:
Com o título, calculemos a entalpia em 2, assim:
No estado 3, conseguimos calcular a entalpia da seguinte forma:
Tendo, , teremos apenas que substituir, assim:
Já vamos aproveitar e calcular o trabalho da bomba, temos:
Passo 3
Aplicando um balanço de energia, conseguimos encontrar a entalpia em 4, assim:
Substituindo,
Bora lá, ao montar o diagrama T-s como foi pedido, teremos o seguinte:
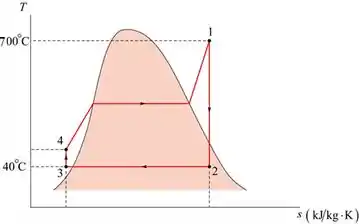
Assim, calculando a produção de trabalho da turbina, teremos:
A produção líquida será:
A entrada de calor é dada por:
Logo, a eficiência do nosso ciclo:
Resposta
A eficiência é de 42,76%.