A Fig. P8.13 mostra os dados de operação em regime estacionário de uma planta de potência solar que opera segundo um ciclo de Rankine com Refrigerante 134a como fluido de trabalho. A turbina e a bomba operam adiabaticamente. A taxa de entrada de energia nos coletores a partir da radiação solar é de 0,3 kW por m2 de área de superfície do coletor, com 60% da entrada de energia para os coletores absorvida pelo refrigerante ao passar pelos coletores. Determine a área de superfície do coletor solar, em m2 por kW de potência desenvolvida pela planta. Discuta os melhoramentos operacionais possíveis que poderiam reduzir a área de superfície necessária ao coletor.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
É dado que:
- Entrada de energia para o coletor de radiação solar:
- Radiação absorvida pelo coletor:
Os dados nos diferentes estados são mostrados na tabela abaixo
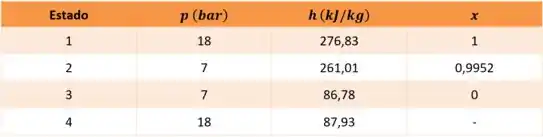
O esquemático é mostrado abaixo
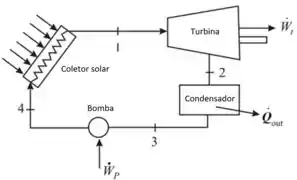
Passo 3
A quantidade de calor absorvido pelo R-134a é
Calculando o trabalho da turbina
Calculando o calor rejeitado no condensador
Passo 4
Calculando o trabalho da bomba
A quantidade de calor adicionado
Passo 5
Para de potência desenvolvida
Calculando a quantidade de calor adicionado
Calculando a quantidade de calor adicionado
Passo 6
Calculando a quantidade de calor absorvida pelo refrigerante