Resolva o problema 9.1 em uma base de ar padrão frio com calores específicos avaliados a 300K
Passo 1
Falaaa galerinha, beleza? Show, primeiro vamos calcular a temperatura em cada estado principal do ciclo. A temperatura dada pela questão.
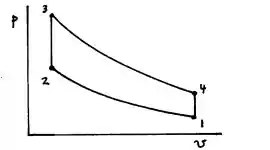
Logo, para o estado 2, dentro de uma compressão isentrópica:
Para o valor de (tabela ), temos:
Para o estado 3, a temperatura pode ser encontrada usando um equilíbrio de energia dentro da transformação do estado 2-3. Temos que:
Mas é igual a 0 porque ganhamos pressão sem aumentar volume. Portanto:
Logo,
No estado 4, para uma expansão isentrópica:
Passo 2
Belezura, bora começar a calcular o que a questão pede. No item a), para encontrarmos o trabalho do ciclo, temos:
Para calcularmos a eficiência térmica, dividimos o trabalho do ciclo pera quantidade de calor na transformação do estado 2 para o 3, logo:
No item c), temos que o deslocamento de volume . Então, o calculo de pressão efetiva pode ser dada por:
Calculando :
Logo, a pressão efetiva é calculada como:
Passo 3
Para os gráficos do enunciado, observem como os valores de trabalho, pressão efetiva e eficiência do ciclo aumentam com base na variação POSITIVA da taxa de compressão.
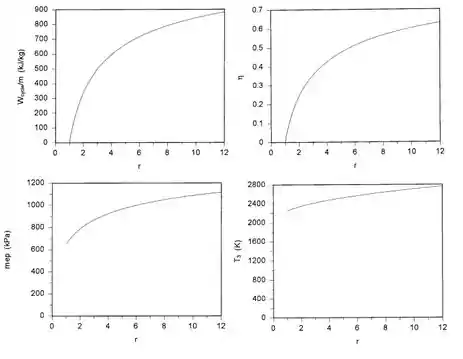
Resposta
Resposta nos passos