Enunciado
Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 136
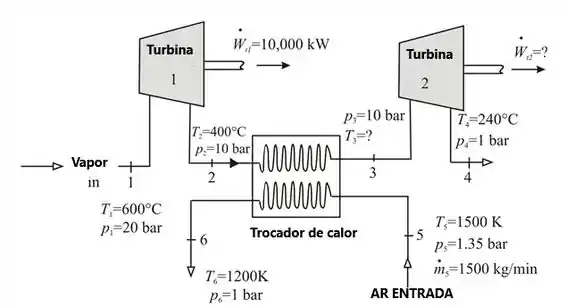
Fluxos separados de vapor e ar escoam ao longo do conjunto turbina-trocador de calor mostrado na Fig. P4.108. Os dados da operação em regime permanente são mostrados na figura. A transferência de calor para o ambiente pode ser desprezada, assim como todos os efeitos das energias cinética e potencial. Determine (a) , em K, e (b) a potência da segunda turbina, em KW.
Passo 1
Falaaaaaaaa queridx’s, bora dar aquele gás?
Então encoxxxta que esse exercício vai ser facinho....
Passo 2
Em “Tabela de vapor superaquecido”
Em “Tabela de vapor superaquecido”
Em “Tabela de vapor superaquecido”
Em “Tabela propriedades gás ideal do ar”
Em “Tabela propriedades gás ideal do ar”
Passo 3
- Pela equação de equilíbrio da taxa de massa
- Pela equação de equilíbrio da taxa de energia para a turbina 2
Passo 4
Pela equação do balanço da taxa de energia para a turbina 1
A taxa de fluxo de massa de vapor é
Passo 5
Usando a equação de equilíbrio da taxa de energia para o trocador de calor
Passo 6
Para , da “Tabela de vapor superaquecido” temos que...
Por interpolação
Passando para K
Portanto a
Passo 7
Portanto a potência da segunda turbina é de
Resposta
- Portanto a .
- Portanto a potência da segunda turbina é de .