Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Termodinamica,Teoria Cinética e Termodinâmica Estatística, Sears e Salinger- Ed: 3º - Capítulo 7.Problemas - Ex. 22

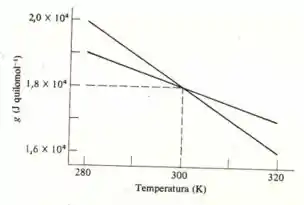
A função de Gibbs específica da fase sólida e da fase líquido de uma substância está representada na figura abaixo em função da temperatura e a uma pressão constante de 10 5   N m - 2 . As pressões mais altas, as curvas de g contra T são paralelas às que estão mostradas. O volume específico molar do sólido e do líquido são respectivamente 0,018   m 3   q u i l o m o l - 1 e 0,020   m 3   q u i l o m o l - 1 .

a) esboce, aproximadamente em escala, curvas de g contra P para as fases sólida e líquida. Justifique as curvas que você traçou.

b) se um quilomol do líquido for super-resfriado até 280   k e, então, transformado em sólido isotérmica e adiabaticamente a 10 ° N   m - 2 , calcule ∆ G ,   ∆ S ,   ∆ H ,   ∆ U   e   ∆ F para o sistema e ∆ S para o universo.

Passo 1

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de termodinâmica de Sears e Salinger a função de Gibbs específica da fase sólida e da fase líquido de uma substância está representada na figura abaixo em função da temperatura e a uma pressão constante de 10 5   N m - 2 . As pressões mais altas, as curvas de g contra T são paralelas às que estão mostradas. O volume específico molar do sólido e do líquido são respectivamente 0,018   m 3   q u i l o m o l - 1 e 0,020   m 3   q u i l o m o l - 1 .

a) esboce, aproximadamente em escala, curvas de g contra P para as fases sólida e líquida. Justifique as curvas que você traçou.

b) se um quilomol do líquido for super-resfriado até 280   k e, então, transformado em sólido isotérmica e adiabaticamente a 10 ° N   m - 2 , calcule ∆ G ,   ∆ S ,   ∆ H ,   ∆ U   e   ∆ F para o sistema e ∆ S para o universo.

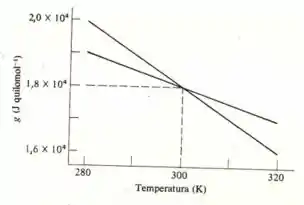
Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.

Passo 2

Então galerinha nessa questão para tratarmos como que será cobrado nas opções temos que antes entender que a função de Gibbs poder ser definida,

∆ G = ∆ H + T ∂ ∆ G ∆ T p

Ficando na letra (a) a representação gráfica das curvas g   e   P com base nos dados fornecidos pelo gráfico no passo anterior é que,

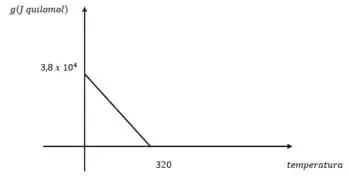
Já na letra (b) para calcular ∆ G ,   ∆ S ,   ∆ H ,   ∆ U   e   ∆ F para o universo sabendo que o líquido foi super-resfriado até 280   K e transformando em sólido isotérmico e adiabaticamente 10 ° N   m - 2 , com isso temos,

∆ G = 1,8   x   10 4 - 1,6   x   10 4 + 280 - 214,285 320 - 300 = - 999,99   ≈ - 10 3   J K

∆ S = 2   x   10 4 - 1 , 8   x   10 4 + 280 - 146,428 3 00 - 280 = - 50   J K

∆ H = 2   x   10 4 - 1,6   x   10 4 + 280 - 1,9   x   10 4 280 = - 1,5   x   10 4   J K

∆ U = 2   x   10 4 - 1 , 8   x   10 4 + 280 1828,57 320 - 280 = - 1,48   x   10 4

∆ F = 2   x   10 4 - 1 , 6   x   10 4 + 280 - 342,857 320 - 300 = - 800   J K

∆ S p a r a   o   u n i v e r s o = 2   x   10 4 + 280 - 2 856,62 320 - 28 0 = - 3,6   J K

Espero que eu tenha ajudado e te vejo no próximo desafio.

Até a próxima.

Resposta

∆ G = - 999,99   ≈ - 10 3   J K

∆ S = - 50   J K

∆ H = - 1,5   x   10 4   J K

∆ U = - 1,48   x   10 4

∆ F = - 800   J K

∆ S p a r a   o   u n i v e r s o = - 3,6   J K

Exercícios de Livros Relacionados

O que significa se o fator de compressibilidade for maior que 1?
Qual é a vantagem dos gráficos generalizados? Quais propriedades devem ser conhecidas além dos próprios gráficos?
Em quais estados os termos de partida para h e s são pequenos? O que é Z aí?
O volume especifico tende a infinito quando a pressão tende a zero. O volume específico tende a zero quando a pressão tende a infinito?
Qual é o benefício da regra de Kay em comparação com uma equação de estado de mistura?